Ce billet est initialement paru sur le blog DMI (Divertissements mathématiques mais (surtout) informatiques)

Ce billet est la suite de Problèmes de transvasements I

Résolution générale : graphes

Les configurations sont maintenant les nœuds d’un graphe. Deux nœuds sont reliés si on peut passer d’une configuration à l’autre en une étape simple qui peut être :

Ces 6 choix correspondent aux trois directions privilégiées du billard-parallélogramme (voir la première partie), prises dans un sens ou dans l’autre.

En s’inspirant d’algorithmes de calcul de plus courts chemins, nous pouvons calculer la méthode la plus rapide pour atteindre n’importe quelle configuration atteignable, en partant du nœud (0,0).

L’idée est de diffuser à partir du nœud de départ, et de toucher toutes les configurations atteignables parmi les 6 envisageables.

La première étape explore les sommets atteignables à partir du nœud (0,0).

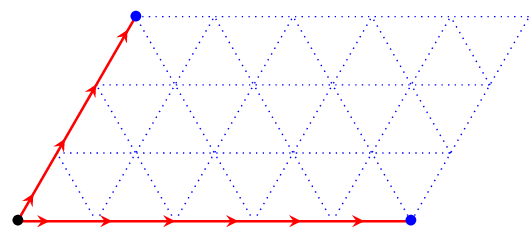
Puis, pour chaque sommet frontière (en bleu), on explore les sommets atteignables.

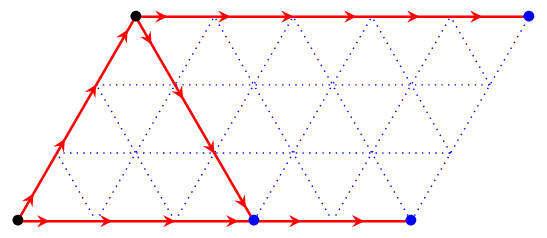
Et ainsi de suite… Si on retombe sur un nœud déjà exploré (ce qui ne manquera pas de se produire), on ne retient ce nouveau chemin que s’il est plus court que celui déjà calculé.

Les calculs sont plus lourds que ceux du programme précédent, mais cette fois, nous explorons :

Le code en question peut être téléchargé ici : transvasements.py

Il contient toutes les fonctions et procédures utilisées plus loin dans ce billet et en particulier la fonction explore

>>> import transvasements as trans
>>> c = trans.explore((0, 0), (5, 3))
>>> print(c)
    {(0, 1): [(5, 1), 5], (4, 3): [(5, 2), 6], (0, 0): [None, 0], (3, 3): [(3, 0), 3], 
     (3, 0): [(0, 3), 2], (2, 0): [(2, 3), 3], (1, 3): [(1, 0), 7], (2, 3): [(5, 0), 2], 
     (5, 0): [(0, 0), 1], (1, 0): [(0, 1), 6], (5, 1): [(3, 3), 4], (0, 3): [(0, 0), 1], 
     (4, 0): [(4, 3), 7], (5, 2): [(0, 2), 5], (0, 2): [(2, 0), 4], (5, 3): [(5, 0), 2]}

Le résultat est un dictionnaire qui nous indique que le sommet (0,1), par exemple, est atteint en 5 étapes en venant du sommet (5,1).

>>>  print(c[(5, 1)])
    [(3, 3), 4]

Le nœud (5,1) est lui même atteignable en 4 étapes (logique…) en venant du sommet (3,3).

Avec l’aide du module pygraphviz (qui fonctionne avec le logiciel Graphviz), on peut facilement transformer cette représentation riche, mais peu lisible, en un graphe :

>>> trans.chemin_graphe(c, "graphe.png")

On obtient alors ce type de graphe, indiquant comment naviguer vers chaque configuration :

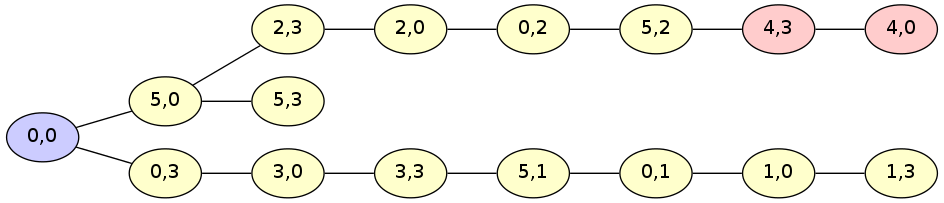
Nous remarquons que deux configurations permettent de faire 4 litres. La plus rapidement atteinte est (4,3) en 6 opérations. Si on veut _partager _les 8 litres en deux, il faut utiliser la solution en 7 coups qui mène à la configuration (4,0), car alors, les 4 litres restants seront dans le récipient de 8 litres. C’est très exactement la manipulation qui est proposée par Guyot (voir le billet précédent)

Les configurations difficiles

Gruber, le terroriste de Die Hard, ne disposant que des deux récipients de 5 et 3 litres, a-t-il eu raison de faire une bombe qui se désamorce avec 4 kg (rappelons que dans Die Hard, il ne s’agit pas de vin ou de liqueur, comme dans les problèmes de Chuquet et Guyot, mais d’eau (encore qu’il soit nécessaire de négliger le poids du bidon utilisé)) ? Un coup d’œil sur le graphe précédent nous permet, pour chaque volume à obtenir, d’indiquer en combien d’étapes il peut être atteint, en faisant au mieux :

Le volume le plus difficile à obtenir était bien 4 litres (Gruber est très méchant).

Mais qu’en serait-il pour d’autres récipients ? Posons nous la question suivante : pour 2 volumes X, Y donnés (X, Y premiers entre eux), quel est le volume atteignable le plus difficile à atteindre ? Et en combien de coup ?

Pour apporter une réponse expérimentale, de manière un peu systématique et graphique, nous allons commencer par numéroter les couples de volumes de récipients (X,Y) avec X>Y , X et Y premiers entre eux :

Les couples sont générés dans l’ordre par ce code :

from math import gcd
for x in range(3, 15):
  for y in range(2, x):
     if gcd(x,y) == 1:
         print((x, y))

L’ordre est celui qu’on obtient en plaçant tous les couples (X,Y) avec X>Y>1 en triangle. Puis on lit ligne à ligne en ne conservant que les couples tels que X et Y soient premiers entre eux (en rouge) :

Pour le couple n, quel est le nombre minimum d’opérations nécessaires un pour atteindre le volume le plus difficile à atteindre ?

Cette suite est facile à calculer si nous disposons des bons outils. La fonction creation_couples (disponible dans le code téléchargeable un peu plus haut) permet de créer les couples (X,Y). On lui donne en paramètres le nombre de couples à générer :

>>> trans.creation_couples(10)
   [(3, 2), (4, 3), (5, 2), (5, 3), (5, 4), (6, 5), (7, 2), (7, 3), (7, 4), (7, 5)]

Puis on recherche la longueur du plus courts court chemin menant à chaque volume atteignable. Par exemple, pour le couple (5,3) :

>>> c = trans.explore((0, 0), (5, 3))
>>> trans.volumes_atteignables(c)
   [0, 4, 2, 1, 6, 1]

On relève dans la liste r, en position k, le nombre d’étapes minimum pour construire le volume k. Ce sont bien les résultats lus un peu plus haut sur le graphe : 4 étapes minimum pour obtenir 1 litre, 2 étapes minimum pour obtenir 2 litres, une seule pour obtenir 3 litres etc.

Le court programme suivant calcule donc les 500 premiers termes de la suite un du nombre d’étapes nécessaires pour obtenir le volume le plus difficile à obtenir (en terme de nombres d’étapes) en utilisant le couple de récipients numéro n.

listecouples = trans.creation_couples(500)
resultats = []
for i, k in enumerate(listecouples):
    c = trans.explore((0, 0), k)
    r = trans.volumes_atteignables(c)
    resultats.append((max(r), tuple(k for k in range(len(r)) if r[k] == max(r))))

Voici les 20 premiers termes :

>>> [r[0] for r in resultats[0:20]]
     [2, 4, 4, 6, 6, 8, 6, 8, 8, 10, 10, 10, 10, 12, 8, 10, 12, 14, 14, 12]

Cette suite a été enregistrée dans l’Online Encyclopedia of Integer Sequence. C’est la séquence numéro A210466.

Le graphe de la suite est facile à tracer (avec matplotlib par exemple) :

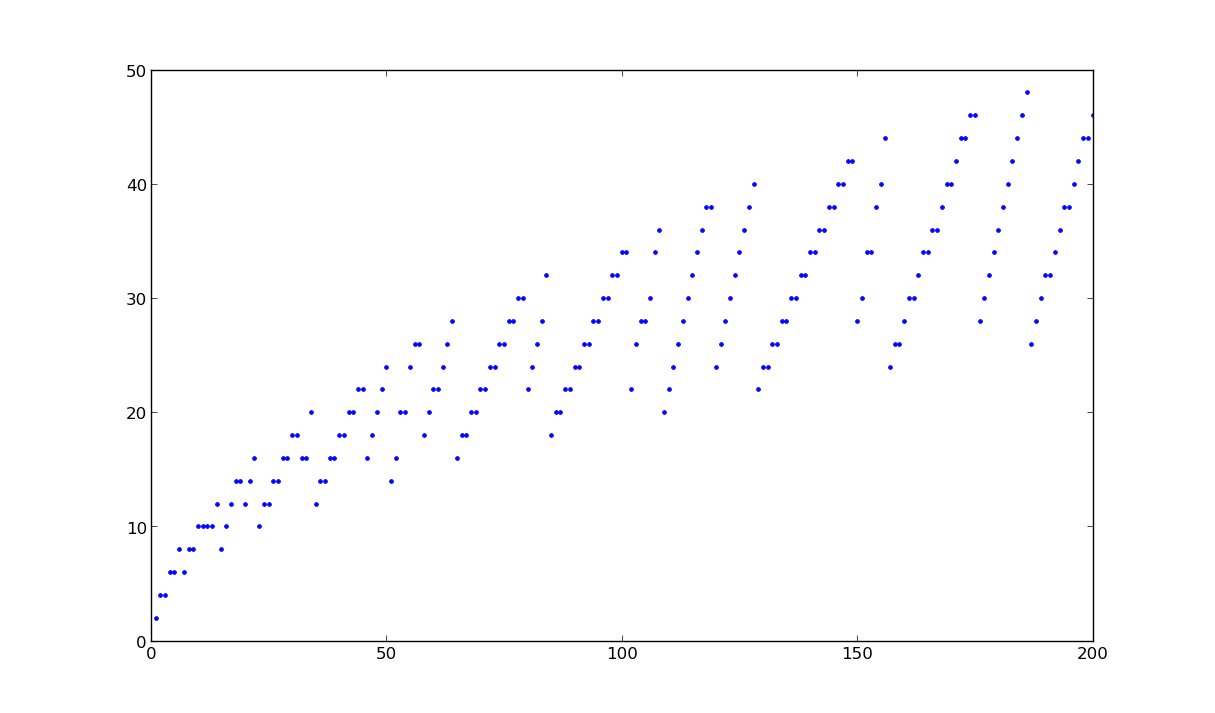
Il présente des régularités étonnantes. Plutôt que de représenter en abscisse le numéro du couple (c’est un peu artificiel), représentons la somme des volumes des récipients (cette idée est suggérée par les dents de scie du graphique, obtenues à chaque changement du volume du plus grand récipient). On obtient le graphique suivant :

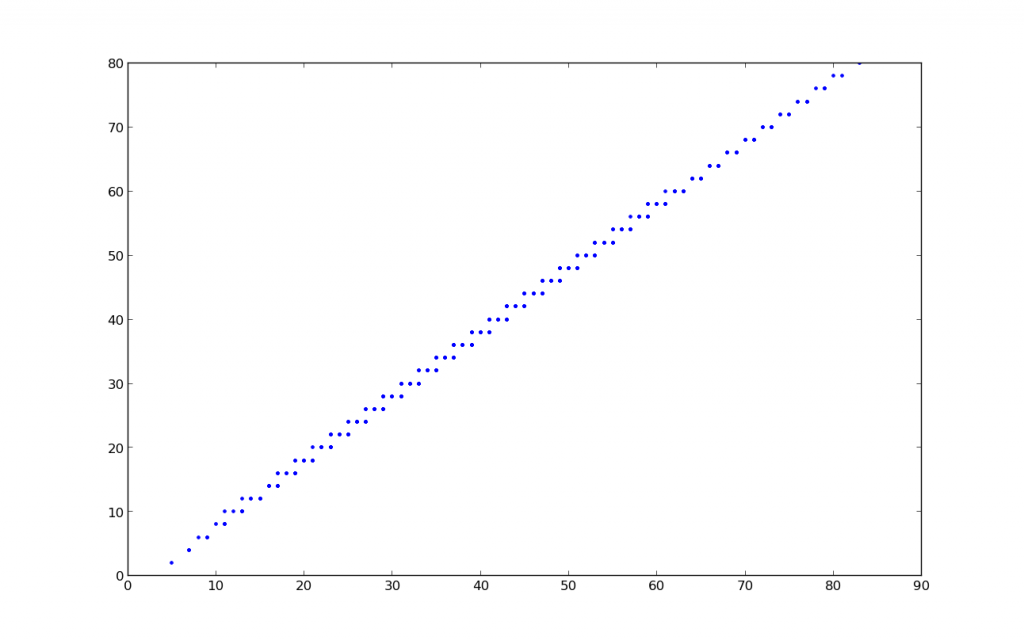
On observe que si l’abscisse m (somme des volumes des récipients) est impaire, on obtient généralement en ordonnée 2 points m-1 et m-3. Si l’abscisse en paire, on obtient généralement m-2. Je dis généralement car il manque des points pour m grand (on les aurait sur la courbe en considérant plus de couples), et pour m petit. On le comprend pour m petit, car il y a peu de couples de nombres satisfaisant aux critères de nos réservoirs dont la somme fait m. Par exemple, il n’y en n’a pas dont la somme fait 6. C’est un peu plus étonnant pour m=15 (on voit qu’il manque un point). Les couples de volumes de réservoir dont la somme fait 15 sont (8,7), (11,4) et (13,2) et dans les trois cas, le volume le plus difficilement atteignable l’est en 12 coups. Il n’y a pas de couple qui donne 14 coups…

Ce graphe permet de conjecturer que pour deux volumes premiers entre eux (x,y), le volume le plus difficile à atteindre pourra être atteint en x+y-2 étapes si x+y est pair et en x+y-1 ou x+y-3 étapes si x+y est impair. Dans le cas impair, si x+y>16, on peut de plus supposer qu’il existe au moins une configuration qui donne la solution x+y-1 et au moins une autre qui donne x+y-3.

Pour les volumes 31 et 37, par exemple, l’observation ci-dessus prévoit que la configuration la plus difficile à atteindre le sera en 66 étapes (31+37-2) :

>>> c = trans.explore((0, 0), (37, 31))
>>> l = trans.volumes_atteignables(c)
>>> max(l)
   66
>>> [i for i in range(len(l)) if l[i] == max(l)]
   [34]

Sur le même principe, on peut faire d’autres observations. Si on ne considère que les récipients dont les volumes (x,y) sont distants de 1, comme (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), (8, 7), (9, 8), (10, 9) … (42,41). Alors le volume le plus difficile à atteindre semble systématiquement être le nombre entier le plus proche de (x+y)/4 et le nombre d’étapes nécessaire x+y-3. Par exemple, pour la configuration (42,41), le volume le plus difficile à atteindre est 21 (or, (42+41)/4=20.75) en 80 étapes (42+41-3=80) :

>>> c = trans.explore((0, 0), (42, 41))
>>> r = trans.volumes_atteignables(c)
>>> max(r)
    80
>>> r.index(80)
    21

Pour les récipients dont les volumes (x,y) sont distants de 2, comme (5, 3), (7, 5), (9, 7), (11, 9), (13, 11), …, (41, 39) alors le volume le plus difficile à atteindre semble être (x+y)/2, et il semble être atteint systématiquement en x+y-2 étapes (ce dernier point est une conséquence des observations précédentes). On retrouve le résultat pour les récipients (5,3), avec un volume de 4 atteignable en 6 étapes.

Naturellement, ces résultats ne sont pas des preuves, mais juste des observations faites à partir de programmes. Il ne reste plus qu'à fournir les démonstrations (elle sont peut être faciles à trouver) ou à dénicher un contre-exemple.

Les graphes à 3 récipients

Les programmes donnés précédemment permettent de construire le graphe des configurations atteignables avec trois récipient aussi, par exemple : 3, 5 et 17 litres que l’on peut remplir à une source intarissable. Le graphe obtenu est relativement grand (cliquez dessus pour zoomer) :

Graphe pour 3 récipients de 3, 5 et 17 litres

Graphe pour 3 récipients de 3, 5 et 17 litres

Il ne comporte pas de longues branches, ce qui est un peu décevant. En particulier, tous les volumes de 1 à 17 litres sont atteignables en 6 opérations au pire (le maximum est atteint pour 16 litres). Il permet néanmoins de lire les solutions pour obtenir n’importe quelle configuration.

Par exemple la configuration (2,5,14) est atteignable en 8 coups (le chemin est coloré dans l’image du graphe) :

Cette dernière section n’est là que parce que je trouve le graphe très joli…