Problèmes de transvasements (première partie)

Une fois n’est pas coutume (encore qu’avec le rythme effréné de 3 billets par an, je ne suis pas sûr qu’on puisse parler de coutume…), ce billet paraîtra en plusieurs parties (sans doute 2), car il est un peu long.

Énoncé du problème

On désire mesurer une certaine quantité de liquide (disons 4 litres) à partir de récipients non gradués de 5 et 3 litres.

Dans les énoncés qui suivent, on trouve deux variantes, selon que les récipients de 5 et 3 litres sont remplis et vidés dans un autre récipient de 8 litres (versions de Bachet et Guyot) ou sont remplis et vidés dans un récipient de grande contenance, dont le volume final ne nous intéresse pas (versions de Chuquet et McLane, le temps d’une alliance improbable).

Ces deux énoncés sont presque équivalents. Dans le premier cas, on veut partager les 8 litres en 2, ce qui revient à mettre 4 litres dans le récipient de taille 5 et 0 dans celui de taille 3 (alors nécessairement le récipient de 8 litre en contiendra 4). Dans le second cas, on veut juste produire 4 litres. Le contenu du plus petit récipient n’est donc pas forcément 0.

Dans la suite, nous nous intéressons plus spécialement à la seconde variante. Mais auparavant retrouvons ce problème dans quelques ouvrages célèbres.

Un problème ancien toujours à propos

Les problèmes de transvasement sont des divertissements mathématiques anciens. On en trouve par exemple un dans l’ouvrage de Nicolas Chuquet : Triparty en la science des nombres. Cet ouvrage manuscrit, datant de 1484 est maintenant conservé à la BnF. Il a été oublié durant près de 300 ans avant d’être réédité à la fin du 19ème siècle. Dans les Problème numériques faisant suite et servant d’application au Triparty, édition de 1881, on trouve (la lecture n’est pas facile, mais c’est amusant) :

Le jeu du tavernier : Il est ung homme vendant vin lequel na que vne mesure de troys pintes. Survient vng ault home aportant vne mesure tenant 5 pintes Lequel demande au tauernier 4 pintes de son vin. (On demande ?) comant ce tauernier po’ra bailler a laultre ces 4 pintes veu quil na que vne mesure de 3 pintes auec la mesure de laultre qui en tient 5. Response. soit emplye la mesure de 5 Et de ces 5 soit emplye la mesure de 3 Et ces 3 pintes remises au tonneau Et ce qui est en la mesure de 5 soit mys en celle de troys. Puis encores soit emplye la mesure de 5 Et de ces 5 soit remplye la mesure de 3 Et par ainsi en la mesure de 4 ¹ demourront 4 pintes qui est ce que lon demande. Ou ault’ment soit emplye la mesure de 3 et vuydee en celle de 5 Et encores de rechef emplye la mesure de 3 et dicelle emplir celle de 5 Puis vuyder celle de 5 ou tonneau Et 1 pinte qui est demouree en celle de 3 soit mise en celle de 5 et apres soit emply 3 et vuyde en 5 et ce sera fait.

L’édition de 1881 a été complètement numérisée. On peut la consulter sur ZVDD. Le problème du tavernier est situé page 460.

Claude Gaspard Bachet relate un problème similaire dès la première édition (1612) de ses Problèmes plaisants et délectables. Il s’agit du problème III de la seconde partie de l’ouvrage dont voici quelques photographies (de l’édition de 1884, la cinquième) :

Le même problème se retrouve aussi dans les Récréations mathématiques de Guyot, dans leur édition de 1799 :

On retrouve des variantes du problème chez Tartaglia, Cardan, Ozanam… plus ou moins dans les mêmes ouvrages que ceux relatant le Problème de Josèphe

Il existe toutefois des références beaucoup plus modernes, puisque c’est à ce même problème de transvasement que McLane et Carver doivent faire face dans le troisième volet de la tétralogie Die Hard (Une journée en enfer/Die Hard with a Vengeance). Cette fois, il ne s’agit pas de contenter le client d’une taverne mais d’éviter l’explosion d’une bombe dans un jardin d’enfants. C’est du sérieux.

Méthode de résolution manuelle : le billard

Une méthode de résolution consiste à naviguer de configuration atteignable en configuration atteignable. Voyons ce que cela donne, graphiquement, avec deux récipients de 5 et 3 litres, en supposant que les 2 sont initialement vides.

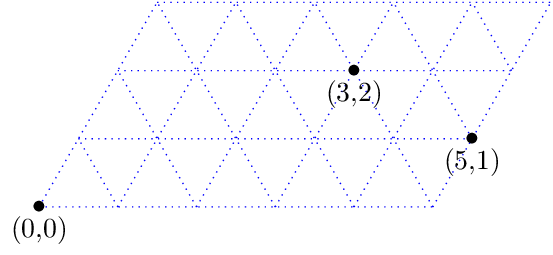
Nous représentons une configuration par un couple de nombres indiquant la quantité de liquide contenue dans chacun des deux récipients. Ces deux nombres vont nous permettre de représenter une configuration par un point du plan. Pour cela, nous utiliserons des axes faisant un angle de 60° (plutôt que les 90° habituels). Dans la figure suivante, trois configurations sont repérées :

• 0,0 (les deux récipients sont vides)
• 3,2 (le grand contient 3 litres et le petit 2 litres)
• 5,1 (le grand récipient est plein, l’autre ne contient qu’un litre)

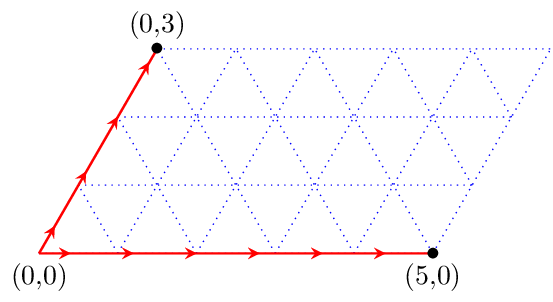
À partir de la configuration de départ (0,0), nous ne pouvons faire que deux choses : remplir l’un ou l’autre des récipients, pour atteindre une des deux configurations (5,0) ou (0,3).

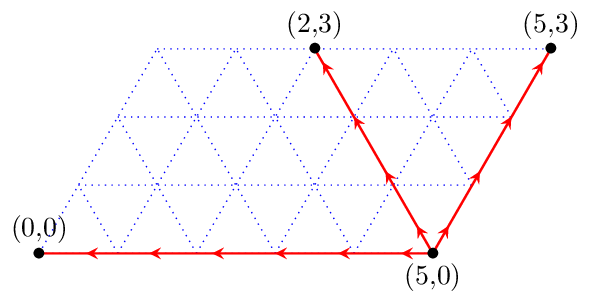
Puis, à partir de la configuration (5,0), nous pouvons atteindre (5,3) en remplissant le second récipient, (0,0) en vidant le premier ou (2,3) en transvasant le premier dans le second.

Depuis une configuration particulière, nous pouvons donc construire d’autres configurations atteignables en une opération unique par un déplacement horizontal ou vertical (qui correspondent à vider ou remplir un des deux récipients) ou selon une diagonale (qui correspond à transvaser un récipient dans un autre). Une fois qu’une direction a été choisie, la configuration atteignable dans cette direction est nécessairement sur le tour du rectangle (5,3), puisque les récipients ne sont pas gradués. Ce qui signifie que l’un des récipients est toujours complètement vide ou complètement plein. Après avoir remarqué que les configurations aux sommets du parallélogramme ne sont pas très intéressantes (elles permettent d’obtenir 0, 3 et 5 litres), nous constatons qu’à chaque configuration, sauf la première (on peut partir vers (5,0) ou (0,3)), il n’y a plus qu’un seul choix de déplacement intéressant :

Ce déplacement est particulièrement visuel dans le cas où les axes sont tracés à 60° car il correspond aux rebonds successifs d’une bille sur un billard en forme de parallélogramme. Cette méthode de résolution du problème s’appelle d’ailleurs : méthode du billard.

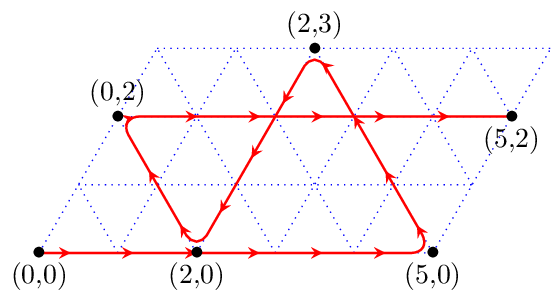
La figure ci-dessous indique la liste des configurations que l’on peut atteindre en commençant par remplir le grand récipient. Le suivi de la trajectoire des configurations nous donne donc les volumes atteignables, et une méthode pour les atteindre (suivre la trajectoire).

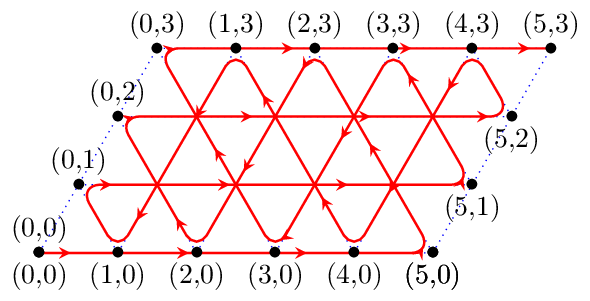
Par exemple, pour obtenir 2 litres dans le petit récipient, le grand étant vide (configuration 0,2), il faut :

• remplir le grand récipient (5,0)
• transvaser le grand dans le petit (2,3)
• vider le petit (2,0)
• transvaser le grand dans le petit (0,2)

Nous voyons aussi que dans le cas particulier de récipients de tailles 5 et 3, toutes les configurations (situées sur le pourtour du parallélogramme) peuvent être atteintes. C’est à dire que n’importe quelle configuration (x,y) où x et y sont entiers, x étant plus petit que 5 et y que 3 sont réalisables.

Ce n’est pas toujours le cas. Par exemple, avec deux récipients de tailles 4 et 6, la trajectoire de la bille sur le parallélogramme donnera :

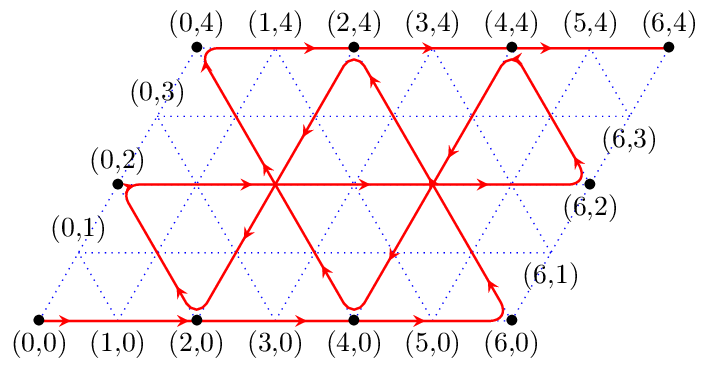
Dans ce cas, seules les configurations pour lesquelles les deux volumes sont pairs sont atteignables. On voit d’ailleurs mal comment il pourrait être possible de mesurer 3 ou 5 litres avec des mesures de 4 et 6 litres uniquement… sauf si un des récipients contient initialement 1 litre, ce qui modifie le point de départ de la trajectoire.

Démontrer de manière rigoureuse à quelle condition toutes les configurations sont atteignables n’est pas évident, même si le résultat semble étonnement familier : le trajet de la bille passera par tous les points du pourtour du parallélogramme si et seulement si les longueurs des côtés sont des nombres premiers entre eux : 3 et 5 sont premiers entre eux, mais 4 et 6 ne le sont pas (2 les divise).

Toutefois, il est possible de donner une sorte de preuve visuelle. Partons du début du trajet (le premier remplissage a été omis pour que le schéma soit plus lisible) :

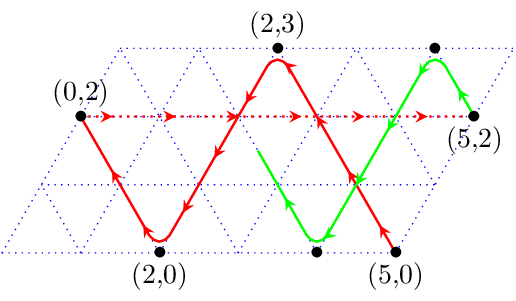
Maintenant, on fait glisser vers la gauche la partie verte de la trajectoire, de manière à amener le point (5,2) sur le point (0,2) :

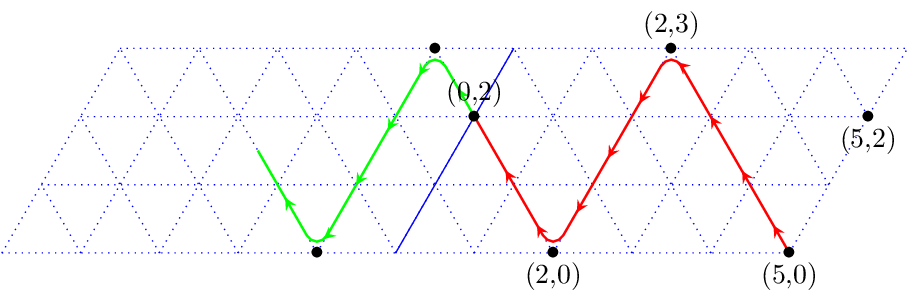
Le trajectoires se raccordent parfaitement et le trajet continue sur le billard recopié à gauche du billard original. On continue de même jusqu’à atteindre le point supérieur gauche (dernière étape avant d’avoir les 2 récipients pleins). Il suffit de 3 glissements de billard ici :

En partant du point le plus à droite, on dessine des rebonds de taille 3 (car le second récipient a pour contenance 3). Le glissement du billard est réalisé de 5 cases en 5 cases. On peut donc faire correspondre les abscisses des points (3, 6, 9, 12, 15) à leurs valeurs sur le billard unique en prenant leur reste dans la division par 5 (on revient à 0 chaque fois qu’on parcourt 5 cases). Ce sont les valeurs entre parenthèses. Notre objectif est de savoir si nous aurons tous les nombres de 0 à 5-1 (4) dans ces parenthèses, ce qui signifiera que tous les points sur le côté inférieur du billard seront touchés.

C’est le cas sur la figure et nous sommes sûr que ce sera le cas si les tailles des récipients sont des nombres premiers entre eux grâce à un résultat d’arithmétique modulaire qui indique que tout nombre p (taille du petit récipient) premier avec n (taille du grand récipient) est générateur du groupe Z/nZ. En d’autres termes, cela signifie que si p est premier avec n, les nombres qui s’écrivent (k.p) % n (reste de la division par n du nombre k fois p), pour k de 1 à n sont exactement les nombres de 0 à n-1 (mais dans le désordre) :

• (1 . 3 ) % 5 = 3
• (2 . 3) % 5 = 1
• (3 . 3) % 5 = 4
• (4 . 3 ) % 5 = 2
• (5 . 3 ) % 5 = 0

Premier algorithme de résolution

Un premier algorithme, directement tiré des rebonds de la bille permet de résoudre le problème. Il consiste à réaliser les opérations suivantes :

• si le grand récipient est vide, le remplir (déplacement vers la droite)
• sinon, si le petit récipient est plein, le vider (déplacement vers le bas-gauche)
• sinon, remplir le petit récipient avec le grand (déplacement vers haut-gauche)

Il est facile de vérifier que ceci donne la trajectoire de la bille.

Voici l’algorithme codé en Python :

def billard(bornes):
    config = [0,0]
    bornes = list(reversed(sorted(bornes)))
    while config != bornes:
        if config[0] == 0: 
            config[0] = bornes[0]
            print("Remplir le grand : ", config)
        elif config[1] == bornes[1]:
            config[1] = 0
            print("Vider le petit : ", config)
        else: 
            t = min(config[0], bornes[1] - config[1])
            config[0] -= t
            config[1] += t
            print("Transvaser du grand vers le petit : ", config)

>>> billard((5, 3))

Remplir le grand :  [5, 0]
Transvaser du grand vers le petit :  [2, 3]
Vider le petit :  [2, 0]
Transvaser du grand vers le petit :  [0, 2]
Remplir le grand :  [5, 2]
Transvaser du grand vers le petit :  [4, 3]
Vider le petit :  [4, 0]
Transvaser du grand vers le petit :  [1, 3]
Vider le petit :  [1, 0]
Transvaser du grand vers le petit :  [0, 1]
Remplir le grand :  [5, 1]
Transvaser du grand vers le petit :  [3, 3]
Vider le petit :  [3, 0]
Transvaser du grand vers le petit :  [0, 3]
Remplir le grand :  [5, 3]

On retrouve la première solution donnée par Chuquet (et employée par McLane) : (0,0) (5,0) (2,3) (2,0) (0,2) (5,2) (4,3)

Si l’objectif est de partager les 8 litres d’un troisième récipient, c’est la configuration (4,0) qu’il faudra atteindre : (0,0) (5,0) (2,3) (2,0) (0,2) (5,2) (4,3) (4,0) ou en partant de la fin : (0,0) (3,0) (3,3) (5,1) (0,1) (1,0) (1,3) (4,0)

Ce sont les deux solutions proposées par Bachet, la seconde étant aussi donnée par Chuquet.

Si le programme précédent nous permet d’atteindre effectivement toutes les solutions, nous allons toutefois jeter un œil à une autre méthode de résolution, moins imagée (plus de billard en forme de parallélogramme), mais plus générale, basée sur l’exploration de graphes.

Elle nous permettra de produire des graphiques indiquant la méthode la plus rapide pour atteindre n’importe quelle configuration atteignable :

La solution donnée le long de la branche du bas est la solution proposée par Bachet pour partager 16 litres en deux parties égales en utilisant une mesure de 9 et une mesure de 7. Quinze étapes sont nécessaires. McLane y a échappé.

Problèmes de transvasements II