Une anamorphose (source : tlfi) est une déformation d’images, de telle sorte que ou bien des images bizarres redeviennent normales ou des images normales deviennent bizarres quand elles sont vues à une certaine distance et réfléchies dans un miroir courbe.
Une anamorphose très connue qui ne nécessite pas de miroir déformant, mais simplement un angle de vue particulier, est celle présente sur le tableau ‘les Ambassadeurs’ peint par Hans Holbein le Jeune en 1533 et exposé à la National Gallery à Londre. Ce tableau peut être observé en utilisant le Google art project. La partie inférieure du tableau est représentée ci-dessous :

La forme allongée est un crâne qui apparaît sans déformation en vue rasante (ci-dessous l’image déformée à l’aide d’un logiciel de retouche d’images, pour simuler la vue rasante) :

Les anamorphoses continuent de fasciner et sont utilisées par des artistes contemporains, par exemple Denis Loquet : http://www.anamorphoses-coniques.com/
Les calculs (et tracés) de plusieurs types d’anamorphoses sont décrits dans les « Récréations mathématiques et physiques » d’Ozanam. Voici les quelques pages et la planche qui détaillent le tracé des anamorphoses visibles dans un miroir conique (les pages qui suivent ont été scannées dans l’édition de 1790 des récréations mathématiques et physiques) :



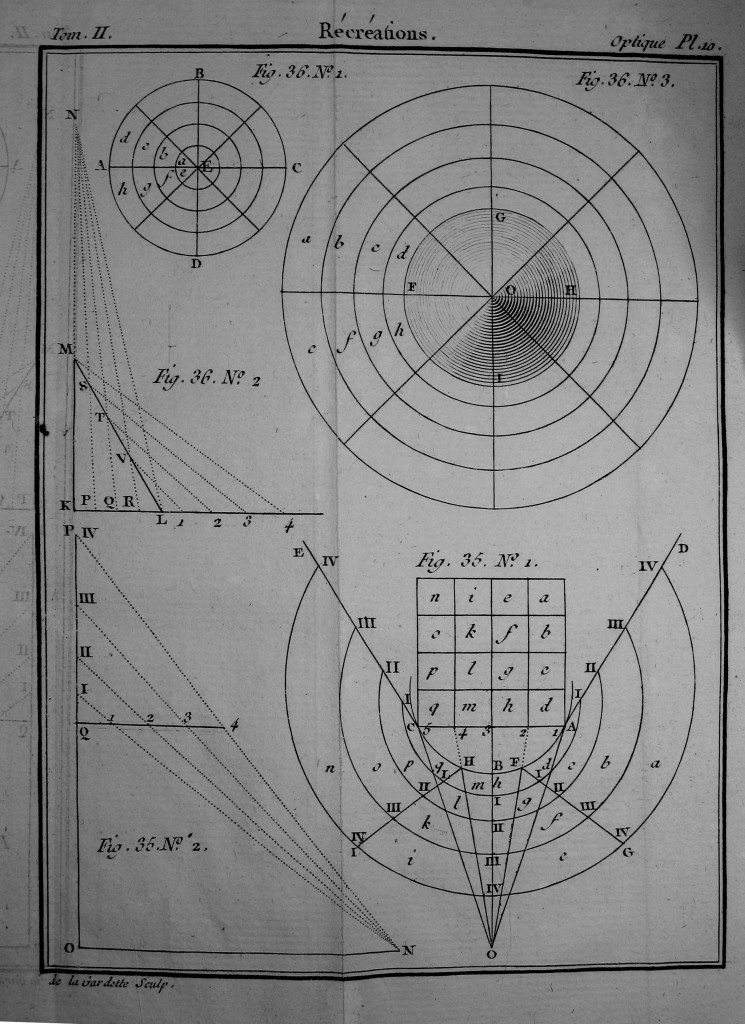
Le programme Python anamorphose.py permet de calculer la déformation d’une image de telle manière qu’après réflexion dans un miroir conique, elle retrouve sa forme originale (par rapport au texte d’Ozanam, on fait l’approximation que l’œil est loin de la pointe du cône).
Voici un exemple d’image calculée par ce programme (l’image d’origine est une partie du tableau “La Naissance de Vénus” de Sandro Botticelli) :

Anamorphose obtenue avec le programme python (anamorphose.png)
Cette image a été imprimée, et un miroir conique (qui ne court pas les rues, je l’admets) a été déposé dessus. Voici une photographie du résultat obtenu, sous plusieurs angles.

Anamorphose 1 (Photo)
La vue de dessus nous restitue une image non déformée (exceptée exactement en son centre, du fait de la difficulté à obtenir un pointe parfaite au sommet du cone).

Anamorphose 2 (Photo)
À défaut de posséder un miroir conique, il est possible d’obtenir des résultats en utilisant un logiciel de lancé de rayon. Un tel logiciel permet de calculer des images synthétiques, à partir de la description d’une scène. Les logiciels de lancer de rayon sont basés sur les lois de l’optique géométrique, qui sont justement celles utilisées dans le calcul d’anamorphoses (qui sont de simples réflexions). Le logiciel de lancer de rayon Pov-Ray, multi plate-formes et gratuit, va nous permettre de calculer le rendu de la réflexion de notre image déformée dans un miroir conique, sans pour autant disposer d’un tel miroir.
Le script som_anmorphose.pov est une description de scène écrite dans le langage que comprend Pov-Ray. On y repère le chargement de l’image déformée, et le cône, avec un rendu métallique. L’image de l’anamorphose, nécessaire au tracé de l’image, est « anamorphose.png » qui peut être téléchargée un peu plus haut dans ce billet.
L’exécution de ce script (taper : povray sim_anamorphose.pov après avoir installé povray, téléchargé le script sim_anamorphose.pov et l’image anamorphose.png) permet d’obtenir des images comme celles ci-dessous, en faisant varier la position de la caméra :

Anamorphose 1 (image calculée)

Anamorphose 2 (image calculée)
Toujours avec Pov-Ray, il est possible de réaliser des animations. On fait varier légèrement un des paramètres (par exemple la position de la caméra) et à chaque variation, une image est calculée.
Toutes ces images sont ensuite mises bout à bout, pour obtenir une petite vidéo comme celle-ci video 800x600 à télécharger

Animation réalisée avec Povray
