Ce billet est initialement paru sur le blog DMI (Divertissements mathématiques mais (surtout) informatiques)

En feuilletant un exemplaire des «Récréations et problèmes mathématiques des temps anciens et modernes» de Rouse Ball (3e édition française, 1898), je suis tombé sur le problème de la souricière (Mousetrap).

De loin, il ressemble un peu au problème de Josèphe. En outre, si le programmer reste facile et intéressant, il n’est pas évident qu’il soit possible de le traiter complètement de manière analytique. Et pour cause… en recherchant un peu dans la littérature, il semble que ce problème soit toujours d’actualité au XXIe siècle, ce qui ne manque pas de m’émerveiller.

Voici un scan des pages de l’ouvrage de Rouse Ball. J’y ai laissé les corrections (justes) faites au crayon par un précédent propriétaire:

Récréations et problèmes mathématiques - Rouse Ball

En résumé, la souricière avec n (par exemple n=5) cartes numérotées de 1 à n consiste à :

Si lors de décompte, on arrive en fin de paquet, on continue de compter en reprenant sur la première carte. Si ce n’est pas clair, il y a une vidéo un peu plus bas…

Deux choses peuvent se produire :

  1. toutes les cartes sont retirées du paquet.
  2. à un moment, on arrive à prononcer le nombre k, avec k>n, ce qui signifie qu’on ne peut plus retirer de cartes.

Le problème est dû à Cayley qui l’a publié en 1878 dans la revue Quarterly Journal of Mathematics.

Les réussites et les jeux gagnants

Retirer une carte du jeu s’appelle faire une réussite. On s’intéresse aux agencements de n cartes qui permettent de faire n réussites (c’est à dire de retirer toutes les cartes). Un tel agencement de départ (n cartes donnant lieu à n réussites) est appelé un jeu gagnant.

Dans notre exemple cela donne :

La disposition 4, 2, 3, 5, 1 donne donc lieu à 5 réussites. C’est un jeu gagnant.

Par contre, la disposition 4, 2, 5, 3, 1 ne donne lieu qu’à 2 réussites:

Bon… et le prog alors ?

Voici un programme Python qui simule des réussites:

def enleve(l):
    if not l : return None, []
    for i in range(max(l)):
        p = i % len(l)
        if l[p] == i + 1:
            return l[p], l[p+1:] + l[:p]
    return None, l

def reussite(l):
    reformed = []
    nbr = 0
    while True:
        val, nl = enleve(l)
        if val is not None :
            nbr = nbr + 1
            reformed.append(val)
        else: return nbr, reformed
        l = nl

la fonction enleve sur une liste de cartes l commence à compter 1 sur la première carte de la liste. Elle renvoie None, liste non modifiée si la partie est finie et carte retirée, nouvelle liste si une carte a pu être enlevée. Auquel cas la nouvelle liste commence exactement sur la carte qui suit la carte qui a été retirée.

La fonction reussite retire des cartes tant que c’est possible. Elle renvoie le nombre de cartes retirées, et la liste des cartes qui ont été retirées, dans l’ordre où elle l’ont été.

Sur les exemples précédent, cela donne:

>>> reussite([4, 2, 3, 5, 1])
    (5, [2, 4, 5, 1, 3])

>>> reussite([4, 2, 5, 3, 1])
    (2, [2, 4])

Voyons si on peut retrouver les résultats donnés par Rouse Ball. Combien de permutations de 4 cartes donnent lieu à 0 réussites, 1 réussite, 2 réussites…?

from collections import Counter
from itertools import permutations

res = []
for p in permutations([1,2,3,4]):
    nb, _ = reussite(p)
    res.append(nb)

c = Counter(res)

L’utilisation de Counter n’est pas obligatoire ici, mais c’est l’occasion… Counter est une implémentation, sous forme de dictionnaire, d’un multiset. Les éléments du multiset sont les clés du dictionnaire, et la valeur associée à la clé est le nombre d’apparition de la clé dans le multiset.

On obtient:

>>> print(c)
Counter({0: 9, 1: 6, 4: 6, 2: 3})

Sur les 24 permutations de 4 cartes, 9 dispositions ne permettent aucune réussite, 6 dispositions en permettent une exactement, 3 dispositions en permettent deux et 6 disposition en permettent quatre. La personne qui a corrigé mon exemplaire de Rouse Ball avait bien compté :-)

La figure suivante illustre la répartition du nombre de réussites pour un nombre de cartes allant de 3 à 8. La couleur correspond au nombre de cartes (pour 3 cartes, il faut regarder les bâtons bleu et pour 8 cartes les bâtons magenta). En abscisse, on relève le nombre de réussites et en ordonnée le pourcentage de permutations de n cartes qui présentent ce nombre de réussites. La forme des courbes est toujours la même. Pour un nombre n de cartes, le pourcentage de permutations permettant de faire k réussites décroit quand k augmente. Il vaut exactement 0 pour k = n – 1 (s’il ne reste plus qu’une carte, on est sûr de l’enlever au tour suivant), et la valeur remonte un peu pour k=n. Cette dernière valeur est le nombre de jeux gagnant pour un certain n.

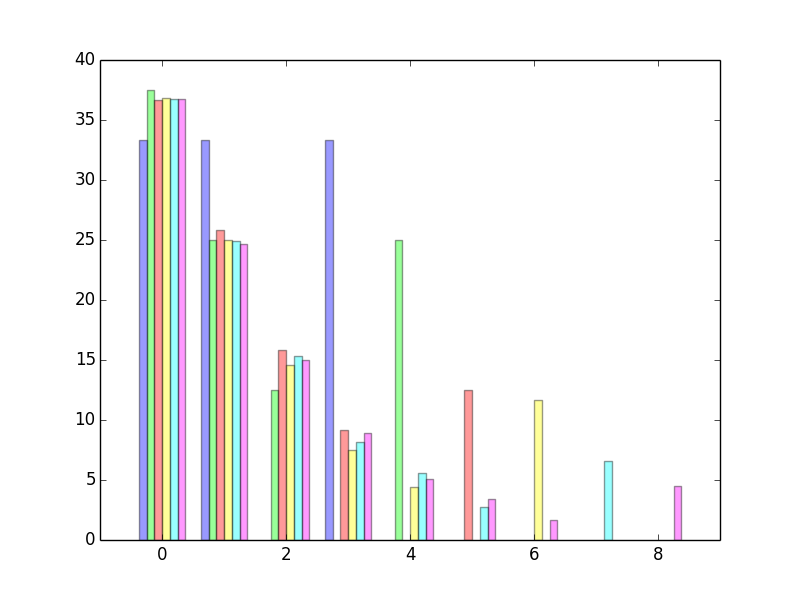
Répartition du nombre des permutations selon le nombre de réussites

En outre, les valeurs obtenues pour k = 0 semblent à peu près constantes quel que soit n. En effet, les cas où on ne peut faire aucune réussite (k=0) sont obtenus si la permutation est un dérangement (un dérangement est une permutation qui ne laisse aucun élément à sa place). Or le nombre de dérangements pour n élément vaut : $N_n = n!\sum_{i=0}^n\frac{(-1)^i}{i!}$

La proportion du nombre de dérangement (par rapport au nombre de permutations qui vaut n!) est donc :$P_n = \sum_{i=0}^n\frac{(-1)^i}{i!}$

Or, $P_n$ tend vers $\frac{1}{e}\approx 0.368$ lorsque n tend vers l’infini, et il le fait relativement vite, $P_3$ valant déjà $\frac{1}{3}$.

La même chose semble se produire pour la proportion de permutations qui donnent lieu à une seule réussite, et cette proportion semble se stabiliser entre 24% et 25%. Je n’ai pas d’explication. Avis aux amateurs… Idem pour 2, 3… réussites ?

Cette simulation permet de relever le nombre de jeux gagnant pour n allant de 3 à 8 (pour n=1, c’est 1… et pour n=2, c’est 1 aussi). On a donc en partant de n=1: 1,1,2,6,15,84,330,1812

Cette séquence est la séquence A007709 de l’OEIS, qui donne toutes les valeurs jusqu’à n=16. Avis aux amateurs qui trouveraient un moyen efficace de pousser le calcul (voir plus loin les travaux de A. Bersani).

Et maintenant ?

Les derniers travaux sur le problème MouseTrap semblent être dûs à Alberto Bersani : On the game MouseTrap.

En particulier, il est l’auteur d’une méthode qui permet de compter le nombre de jeux gagnant pour n cartes, sans toutefois énumérer les n! configurations de départ. En effet, avec le programme précédent, on peut difficilement espérer atteindre n=10. La méthode proposée par Bersani (qu’il appelle approche eulérienne) lui a permis d’aller jusqu’à n=16 (et de compléter la séquence A007709 sur l’OEIS)

Voici quelques autres ramifications du jeu.

Réussite dans l’ordre

Pour un nombre de cartes particulier, on s’intéresse à la permutation de départ particulière qui permet de retirer toutes les cartes dans leur ordre naturel (la carte 1 en premier, puis la carte 2 etc…).

C’est facile à faire à la main, mais voilà tout de même un petit programme:

def reussiteordre(n):
    res = [None] * n
    index = 0
    for i in range(1, n + 1):
        libres = [j for j in range(n) if res[j] is None]
        pos = libres.index(index)
        pos = (pos + (i-1)) % len(libres)
        index = libres[pos]
        res[index] = i
        index = libres[(pos + 1) % len(libres)]
    return res

>>> reussiteordre(8)
    [1, 6, 2, 4, 5, 3, 7, 8]

L’ordre des 8 cartes donné ci-dessus permet donc de faire 8 réussites, en imposant de plus que les cartes soient retirées par ordre croissant. Mon programme n’est pas très joli.

Permutations reformantes

On s’intéresse uniquement aux jeux gagnants de n cartes (qui donnent donc lieu à n réussites). Dans ce cas, l’ordre de sortie des cartes est une nouvelle permutation. Et cette nouvelle permutation… est-ce aussi un jeu gagnant ? Et ça va durer encore longtemps ? 😀 Les permutations 1-reformantes (1-reformed decks) sont les jeux gagnants dont la permutation résultante (l’ordre de sortie des cartes) n’est pas un jeu gagnant. Une permutation est k-reformante (k>1) si c’est un jeu gagnant et que la permutation résultante et (k-1)-reformante.

Le programme suivant calcule la valeur de k pour une permutation donnée (k = 0 si la permutation ne donne pas lieu à n réussites).

def rank(l):
    nb = len(l)
    rk = 0
    while True:
        n,l = reussite(l)
        if n < nb: return rk
        rk += 1

Pour 5 cartes le mieux qu’on puisse avoir est une permutation 2-reformante. Il n’y en a qu’une et c’est (2, 5, 1, 4, 3). En effet, elle donne lieu à 5 réussites, et les cartes sont retirées dans l’ordre : (4, 2, 3, 5, 1). Et cette permutation donne elle même lieu à 5 réussites. Les cartes sont retirées dans cet ordre : (2, 4, 5, 1, 3). Cette permutation, par contre, ne donne lieu à aucune réussite.

En 2007, A. Bersani a exhibé une permutation 5-reformante pour 16 cartes.

La souricière modulaire

Parmi toutes les variantes de ce jeu, celle-ci semble offrir encore de nouvelles perspectives.

Lorsqu’on démarre avec n cartes, à la souricière modulaire, on autorise, si on a compté jusqu’à n sans enlever de carte, à continuer à compter, en redémarrant sur 1. Dans ce cas, lorsque n est premier, soit on ne fait aucune réussite, soit on en fait n.

Par exemple, pour 4, 2, 5, 3, 1 :

Au jeu de la souricière, cette permutation ne donnait lieu qu’à 2 réussites. Nous en avons 5 au jeu de la souricière modulaire.

On pourrait continuer encore longtemps à trouver des variantes et des simulations à faire… je m’arrête sinon, ce billet ne paraîtra jamais :-)