On entend souvent dire qu’il est facile de faire des erreurs dans les calculs de dénombrements ou de probabilités. Voire que les intuitions que l’on a au sujet de ces problèmes sont souvent trompeuses. C’est bien mon avis aussi. Et justement, j’avais pour projet de faire un petit article illustrant comment conforter ses intuitions, voire ses calculs, en exécutant un programme qui simule les tirages aléatoires.
Idée de départ
Voici quelques exemples de problèmes qui peuvent mettre en défaut votre intuition (si ce n’est pas le cas tant mieux pour vous, vous n’aurez pas besoin d’ordi pour vérifier).
Les dés Toscans
Le problème qui suit a été posé à Galilée par Cosme II de Médicis, grand-duc de Toscane (son ancien élève) au début du XVIIe siècle. Ce dernier, amateur de jeux, avait remarqué qu’en jetant trois dés et en faisant le total, il atteignait plus souvent 10 que 9. Ce résultat lui paraissait contre intuitif car il avait dénombré autant de façons différentes de faire 9 que de faire 10. Galilée répondit à ces interrogations dans un traité rédigé en 1620. Qu’en pensez-vous ?
Les dés d’Efron ou dés intransitifs
Ces dés ont été inventés par Bradley Efron, et sont à l’honneur dans la rubrique Logique et Calcul du magazine Pour la Science d’avril 2013 (n°426). Ils sont aussi utilisés dans une nouvelle de Colin Bruce, dans l’ouvrage Élémentaire mon cher Watson (Flammarion). C’est cette version que je reprends ici.
Ce jeu se joue avec 3 dés. Le dé A a été imprimé 6 fois avec un 4 (les 6 faces sont identiques). Le dé B a 2 fois le chiffre 10 et 4 fois le chiffre 1. Et enfin le dé C a 4 fois le chiffre 6 et 2 fois le chiffre 0. Le total sur chaque dé vaut donc 24, ce qui implique que la moyenne des tirages pour n’importe lequel de ces dés tendra vers 4 si on réalise beaucoup de tirages. Dans ce jeu, deux joueurs prennent chacun un dé et celui qui obtient la plus grande valeur gagne.
Bien que chaque dé produise en moyenne un 4 (tous les dés ont donc l’air équivalents en moyenne), le joueur qui choisit le dé en dernier dispose d’une stratégie qui lui permet de remporter la victoire pratiquement deux fois sur trois. Pensez-vous que ce soit possible ?
Pile ou Face (aka les croissants de Sham and Science)
On lance 10 fois d’affilée une pièce équilibrée, et on souhaite que sur les 10 lancers, il y ait exactement 2 fois face et 8 fois pile. Quelle est la probabilité qu’avec une série de 10 lancers, ceci se produise ? Combien de séries de 10 lancers faudra-t-il réaliser pour qu’il y ait de bones chances (probabilité strictement supérieure à 0.5) que cela se produise au moins une fois ?
Résolution et simulation
Dans les trois problèmes évoqués, il est possible de raisonner, de faire un calcul, et de trouver un résultat. La question est alors la suivante : il est si facile de se tromper dans les problèmes de dénombrements, qu’une fois le calcul terminé, je n’ai qu’une confiance relative dans ce que j’ai fait. Pour me convaincre (dans une certaine mesure) que mon résultat est correct, j’ai pris l’habitude de simuler les évènements dénombrés, en espérant ainsi retrouver numériquement mon résultat.
Il n’est pas non plus exclu de faire en premier la simulation, car la programmer peut parfois aider à mieux identifier les différents cas. Avoir un résultat numérique préalable peut aussi permettre d’orienter la réflexion.
Voyons ce que ça donne sur les problèmes qui précédent.
Les dés Toscans
Reprenons le raisonnement du duc de Toscane. Les différentes façons de faire 9 avec trois dés sont :
6,2,1 – 5,3,1 – 5,2,2 – 4,4,1 – 4,3,2 – 3,3,3
Les différentes façons de faire 10 sont :
6,3,1 – 6,2,2 – 5,4,1 – 5,3,2 – 4,4,2, – 4,3,3
Vous pouvez vérifier, il n’y en a pas d’autres. On a donc autant de façons de faire 9 que de faire 10 (le duc de Toscane en avait dénombré 6). Il semble donc acquis que sur un grand nombre de tirages, on obtiendra à peu près aussi souvent 9 que 10.
Le programme Python qui suit réalise 50000 tirages des 3 dés, et compte le nombre de fois où chaque total est obtenu :
import random
nombre_fois = [0] * 19 # nombre_fois[i] vaudra le nombre de fois où le total i
# a été atteint
for i in range(50000):
des = (random.randint(1, 6) for i in range(3)) # tirage 3 dés
s = sum(des) # somme des 3 dés
nombre_fois[s] += 1
print(list(enumerate(nombre_fois)))
Voilà ce qui s’affiche :
[(0,0), (1,0), (2,0), (3,214), (4,743), (5,1342), (6,2323), (7,3554),
(8,4919), (9,5720), (10,6237), (11,6222), (12,5766), (13,4912), (14,3455),
(15,2284), (16,1382), (17,698), (18,229)]
Attention, la première case est la case 0 et le nombre de fois où le total 9 a été obtenu est 5720. Le total 10 a été obtenu 6237. Si on ramène ça au nombre de tirage, 9 a été obtenu dans 11.44% des cas et 10 dans 12.47%. Ça laisse perplexe. On ne sait pas bien si cet écart est dû au caractère aléatoire des tirages et si en recommençant, on n’obtiendrait pas le contraire… Si on trace un courbe comportant en abscisse un total de 3 à 18 et en ordonnée le nombre de fois où ce total a été obtenu, on obtient ceci :
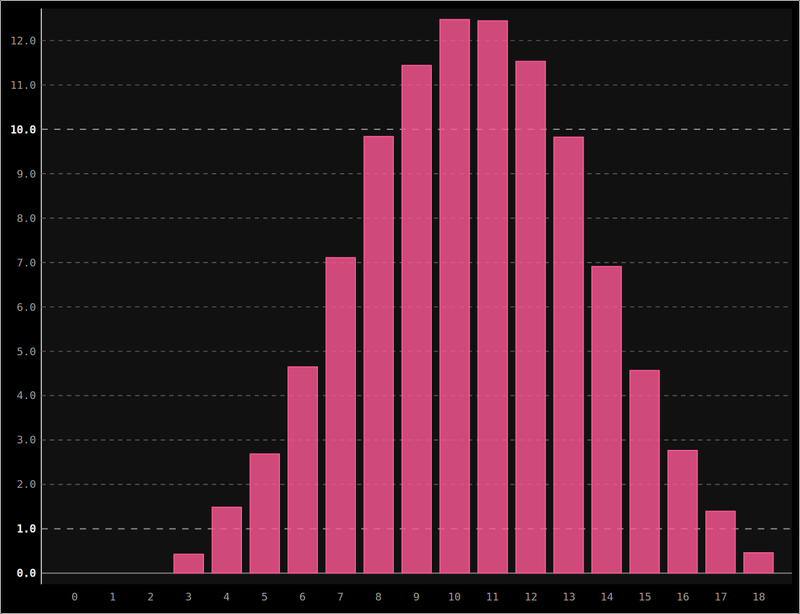
Le doute n’est plus permis, l’allure de la courbe nous montre bien que le nombre de 9 et le nombre de 10 ne se rapprocheront pas en faisant plus de tirage. En outre, on remarque que la courbe est presque symétrique par rapport à 10.5, ce dont on aurait pu se douter en remarquant que la moyenne que l’on obtiendra pour chaque dé est $(1+2+3+4+5+6)/6=3.5$. Pour 3 dés, la moyenne est donc $3\times3.5 =10.5$. Les valeurs des dés étant symétriques autour de 3.5, il est donc logique d’obtenir autant de fois 10 que 11, autant de fois 9 que 12 etc.. mais moins de 9 que de 10.
Le programme ne nous aide pas à trouver notre erreur, mais nous permet d’être sûr que nous en avons fait une (dans ce billet, on part du principe que les erreurs ne sont pas dans les programmes :-)
Le raisonnement peut être corrigé si on imagine par exemple que les dés sont colorés : un bleu, un rouge et un vert. On lance les 3 dés, puis on les met dans cet ordre : le bleu, puis le rouge, puis le vert et on relève ensuite les valeurs des dés, dans cet ordre. Les tirages différents (parfois uniquement par la couleur des dés) qui donnent 9 sont maintenant :
6,2,1 – 6,1,2 – 1,2,6 – 1,6,2 – 2,1,6 – 2,6,1 – 5,3,1 – 5,1,3 – 3,1,5 – 3,5,1 – 1,3,5 – 1,5,3 – 5,2,2 – 2,5,2 – 2,2,5 – 4,4,1 – 1,4,4 – 4,1,4 – 4,3,2 – 4,2,3 – 3,2,4 – 3,4,2 – 2,3,4 – 2,4,3 – 3,3,3
Il y a 25 tirage. Si on reprend notre énumération précédente, chaque fois que les valeurs des dés sont différentes, nous dénombrons 6 tirages (par exemple 6,2,1 – 6,1,2 – 2,6,1 – 2,1,6 – 1,2,6 et 1,6,2).
Lorsque 2 valeurs seulement sont identiques nous dénombrons 3 tirages et lorsque les trois valeurs sont égales, nous avons un seul tirage.
Pour obtenir 10 :
6,3,1 – 6,1,3 – 1,3,6 – 1,6,3 – 3,1,6 – 3,6,1 – 6,2,2 – 2,6,2 – 2,2,6 – 5,4,1 – 5,1,4 – 1,4,5 – 1,5,4 – 4,1,5 – 4,5,1 – 5,3,2 – 5,2,3 – 3,2,5 – 3,5,2 – 2,3,5 – 2,5,3 – 4,4,2 – 2,4,2 – 2,2,4 – 4,3,3 – 3,4,3 – 3,3,4
Il y a 27 tirages.
Le nombre de tirages différents est $6^3$ (6 choix pour le dé bleu, 6 pour le dé rouge etc…). La probabilité d’obtenir un total de 9 (cas favorables / cas possibles) vaut donc $25/6^3\approx 11.57%$.
La probabilité d’obtenir un total de 10 est $27/6^3 = 12.5%$.
On retrouve bien à peu près nos résultats expérimentaux (11.44% et 12.47%) ce qui, à défaut de nous assurer que nos résultats théoriques ($25/6^3$ et $27/6^3$) sont justes, nous permet d’être relativement confiants.
Les dés d’Efron
Rappelons les valeurs des dés :
- dé A : six fois la valeur 4
- dé B : deux fois 10 et quatre fois 1
- dé C : quatre fois 6 et deux fois 0
On nous affirme que quel que soit le dé choisi par le joueur 1, il existe un dé qui permet de le vaincre plus de la moitié du temps. Pour tester ceci expérimentalement, et sans connaître l’éventuelle tactique, nous pouvons pour chaque couple de dé (il y a 3 couples possibles, dés A-B, dés B-C, dés C-A), réaliser 10000 tirages, et voir si un des dés de la paire a une nette victoire :
import random
from itertools import combinations
des={"deA": [4] * 6,"deB": [10, 10] + [1] * 4, "deC": [0, 0] + [4] * 6}
print(des)
resultats=dict()
for dei, dej in combinations(des, 2):
key = dei + "/" + dej
resultats[key] = [0, 0]
for n in range(10000):
ti = random.choice(des[dei])
tj = random.choice(des[dej])
if ti > tj:
resultats[key][0] += 1
else:
resultats[key][1] += 1
print(resultats)
Voici ce qu’affiche ce programme :
{'deA': [4, 4, 4, 4, 4, 4], 'deB': [10, 10, 1, 1, 1, 1], 'deC': [6, 6, 6, 6, 0, 0]}
{'deB/deC': [5569, 4431], 'deA/deC': [3317, 6683], 'deA/deB': [6605, 3395]}
Très nettement, le dé B gagne le dé C (dans 56% des cas), le dé C gagne le de A (dans 67% des cas), et le dé A gagne le dé B (dans 66% des cas). Aucun dé n’est plus fort que les autres, mais chaque dé est plus fort qu’un autre et plus faible qu’un autre. Il semble que les chances de gagner avec un dé fort soit d’environ 2/3 (sauf pour les dés B et C ou la victoire est moins nette).
On peut bien sûr retrouver ces résultats par le calcul :
- entre le dé A et le dé B, le dé B gagne lorsqu’il tombe sur 10 et perd lorsqu’il tombe sur 1. Il gagne donc 2 fois sur 6. Le dé A gagne le dé B 2 fois sur 3.
- entre le dé A et le dé C, le dé C gagne s’il tombe sur 6 uniquement, dont 2 fois sur 3
- entre le dé B et le dé C, on peut raisonner ainsi : dans 2 tiers des cas, le dé C tombe sur 6, et il tombe sur 0 dans un tiers des cas.
Lorsqu’il tombe sur 6, il perd contre le dé B lorsque celui-ci tombe sur 10 (dans 1/3 des cas), et s’il tombe sur 0, il perd tout le temps contre le dé B.
Par conséquent, le dé B perd dans $\underbrace{2/3}_{\mbox{C sur 6}}\times\overbrace{1/3}^{\mbox{B sur 10}}+\underbrace{1/3}_{\mbox{B sur 0}}=5/9$.
On retrouve bien nos résultats expérimentaux : A gagne B deux fois sur trois (nous avions 66%) , C gagne A deux fois sur trois (nous avions 67%) et B gagne C cinq fois sur 9 (nous avions 56%, la valeur théorique étant 55.55..%). On peut même ajouter que bien qu’aucun des dés ne soit plus fort que les autres, le problème n’est pas symétrique et si on est contraint de choisir un dé en premier, et si l’autre joueur joue parfaitement (il sait quel dé choisir), alors on a intérêt à prendre le dé C, qui permet de perdre moins souvent.
Pile ou Face
Cette fois-ci, nous allons d’abord regarder au calcul et ensuite faire une petite vérification par simulation. On s’intéresse à la probabilité de faire exactement deux fois face sur dix lancers d’une pièce. On peut représenter les 10 lancers par une séquence de 10 caractères P ou F.
Par exemple, PPFPFFFFPF correspond à 10 lancers. Les séries de 10 lancers qui nous intéressent sont celles qui comportent exactement 2 fois la lettre F. Il y en a autant qu’on peut écrire de mots comportant 8 lettres P et 2 lettres F. Pour générer une telle série de lancers, la seule chose à choisir est la position des 2 F dans la série. Il y a $C_{10}^2=\frac{10\times 9}{2}=45$ façons de choisir les 2 positions (on a 10 choix pour la première et 9 pour la seconde, et échanger ces deux positions conduit à la même série).
Le nombre de tirages différents (c’est à dire le nombre de mots de 10 lettres comportant des P et des F) est $2^{10}$ puisqu’on a 2 choix pour chaque lancer et qu’on réalise 10 lancers. La probabilité de faire exactement deux faces est donc
$C_{10}^2/2^{10}\approx0.044\approx 4,4%$.
Si on réalise n fois les 10 lancers, on a bien sûr plus de chances de réussir un tirage avec exactement 2 faces. Un erreur serait de penser qu’on a n fois plus de chances.
Par exemple, en réalisant 2 séries de 10 lancers, on n’a pas 8,8% de chances de faire une série avec 2 faces (même si la valeur est proche, elle ne vaut pas
$2\times 4,4%$. Si ce raisonnement était correct, cela signifierait qu’en réalisant 23 séries de 10 lancers, les chances de réaliser une série avec 2 faces
deviendraient supérieures à 100% ($23\times C_{10}^2/2^{10}\geq 1$), ce qui est intolérable :-).
L’astuce pour résoudre le problème est de le prendre à l’envers. Appelons p la probabilité de faire exactement
2 faces dans une série de 10 lancers ($p=C_{10}^2/2^{10}$). La probabilité de ne pas faire exactement deux faces sur 10 lancers est $1-p$.
La probabilité de ne pas faire 2 faces ni dans la première série de 10 ni dans la seconde est $(1-p)(1-p)$.
De même la probabilité de ne pas faire exactement 2 faces dans chacune des n séries de 10 lancers est : $(1-p)^n$.
Le contraire de cet événement est justement de réussir au moins une fois une série de 10 lancers contenant exactement 2 fois face.
La probabilité que cela se produise est donc $1-(1-p)^n$. Après 23 séries de 10 lancers, on trouve que les chances de
réaliser au moins une série comportant exactement 2 faces sont de 62%. Lorsque n devient grand,
la probabilité que nous avons calculé tend vers 1, sans toutefois l’atteindre,
ce qui est satisfaisant. Accessoirement, cette probabilité dépasse
50% à partir de la 16e série de 10 lancers.
La question est maintenant : est-ce que ce calcul est correct ?
Nous pouvons le vérifier (c’est une vérification expérimentale, pas une preuve) en simulant les lancers de pièces :
import random
p=[]
# Pour n séries de 10 lancers, n variant de 1 à 29
for n in range(1, 30):
compte = 0
# On estime la probabilité à partir de 1000 séries
for k in range(10000):
co = False
for i in range(n):
s = sum([random.randint(0, 1) for i in range(10)])
if s == 2: # on a fait un tirage avec exactement 2 faces
co = True
if co: # Au moins une série comporte exactement 2 faces
compte += 1
p.append(( n, compte / 10000, 1 - (1 - 45 / (2 ** 10)) ** n )) # Notre résultat théorique
for v in p:
print("{:02d} series : {:.3f} {:.3f}".format(*v))
Ce programme affiche, selon le nombre de séries de 10 lancers, la probabilité expérimentale, puis théorique (selon notre analyse), de
réussir au moins une fois une série comportant exactement 2 faces.
01 series : 0.040 0.044
02 series : 0.080 0.086
03 series : 0.129 0.126
04 series : 0.164 0.165
05 series : 0.201 0.201
06 series : 0.233 0.236
07 series : 0.272 0.270
08 series : 0.299 0.302
09 series : 0.336 0.333
10 series : 0.357 0.362
11 series : 0.386 0.390
12 series : 0.421 0.417
13 series : 0.441 0.442
14 series : 0.465 0.467
15 series : 0.486 0.490
16 series : 0.511 0.513
17 series : 0.541 0.534
18 series : 0.561 0.555
19 series : 0.578 0.574
20 series : 0.588 0.593
21 series : 0.607 0.611
22 series : 0.621 0.628
23 series : 0.645 0.644
24 series : 0.660 0.660
25 series : 0.673 0.675
26 series : 0.683 0.689
27 series : 0.705 0.703
28 series : 0.717 0.716
29 series : 0.729 0.728
Les séries calculées et mesurées concordent :
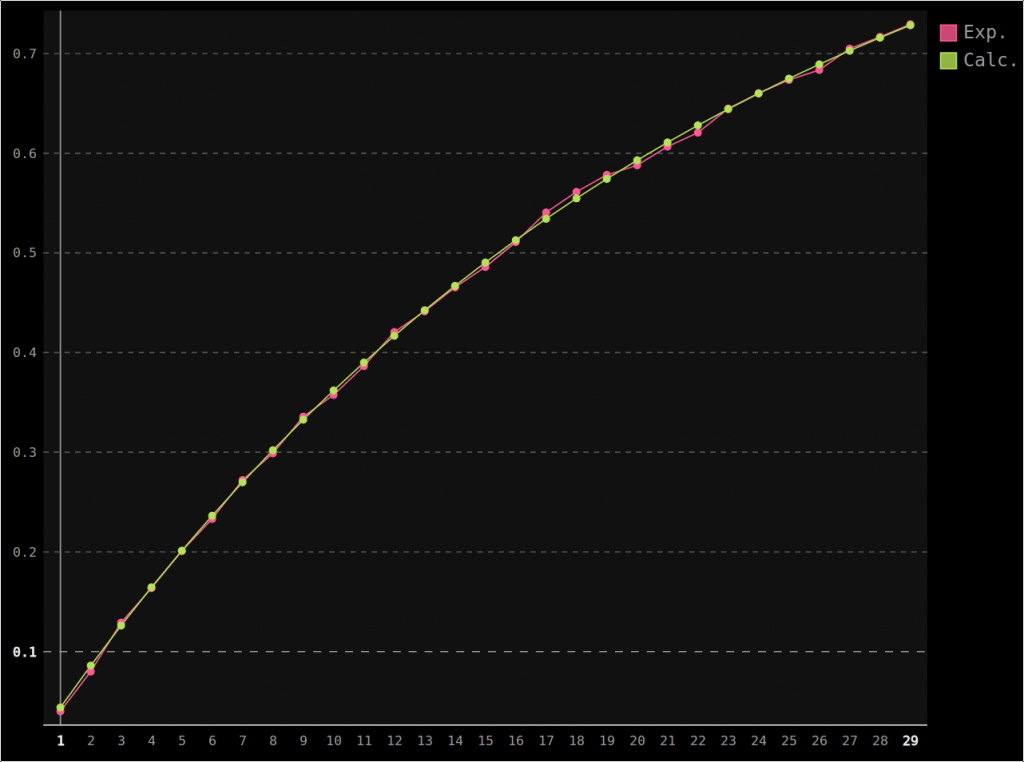
Si on n’était pas très sûr de son raisonnement, obtenir une telle courbe, sans pour autant constituer une preuve, permet d’être assez confiant (et en effet, le raisonnement est juste).
Conclusion
Simuler ce genre d’expériences n’est sans doute pas très glorieux… C’est cependant facile à faire, assez amusant, et peut parfois éviter des erreurs de raisonnement dans les calculs de dénombrement et de probabilité. Pourquoi s’en priver ? Pour vous entraîner, je vous invite à faire ce que suggère Jean-Paul Delahaye dans l'article sur les dés d’Efron (Pour la Science). On considère les 3 dés suivants :
- dé A : 6,3,3,3,3,3
- dé B : 5,5,5,2,2,2
- dé C : 1,4,4,4,4,4
La moyenne de chaque dé est 3.5. On peut vérifier que ces dés sont intransitifs : le dé A gagne plus souvent le dé B, le dé B gagne plus souvent le dé C, et le dé C gagne plus souvent le dé A.
Pourtant, si au lieu de faire un lancer, on en fait 2 (et on compare les 2 sommes), alors l’avantage change de camp, et c’est le dé B qui gagne le dé A, le dé C qui gagne le dé B et le dé A qui gagne le dé C.
C’est un bon exercice que de vérifier ce fait particulièrement contre-intuitif par une simulation.
