Dans ce billet, je vous propose d’utiliser diverses techniques permettant de venir à bout, de manière automatique, d’un texte suffisamment long crypté avec le chiffre de Vigénère. Les thèmes abordés seront : le chiffre de César, l'analyse fréquentielle, le chiffre de Vigénère et l'indice de coïncidence.
Chiffre de César
Avant d’aborder le chiffre de Vigénère, nous allons traiter le cas du chiffre de César, que tout le monde connaît probablement, mais qui nous sera utile dans la suite. Le chiffre de César consiste à crypter un texte en décalant les lettres de 3 positions dans l’alphabet. On trouvera un témoignage de Suétone sur cette pratique dans la Vie des 12 Césars.
Naturellement, le chiffre de César peut être utilisé avec un décalage autre que 3. Nous pouvons même considérer qu’il peut être utilisé avec un décalage n, et que n est la clé qui permet de déchiffrer le message.
Le chiffre de César, à l’époque des ordinateurs, n’est pas très redoutable. Il est très facile et très rapide de tester les 25 décalages possibles, et de ne retenir que le seul qui produit un texte intelligible. Voici une portion de code Python3 qui chiffre une chaîne de caractères (après l’avoir mise en capitales), avec un décalage donné (les caractères qui n’étaient pas des lettres restent inchangés) :
import string
def cesar(chaine,dec):
alph = string.ascii_uppercase
s = chaine.upper()
return s.translate(str.maketrans(alph, alph[dec:] + alph[:dec]))
L’objectif, ici, n’étant pas de présenter le langage Python, j’essaie de donner des implémentations assez concises,
ce qui peut être aussi l’occasion de découvrir de nouvelles fonctionnalités du langage. Remarquons au passage
que dec peut être positif ou négatif et qu’un décalage négatif de -k, avec -26<-k<0 donne la même chose
qu’un décalage de 26-k (décalage qui est positif).
Prenons un texte chiffré (dans lequel on a retiré la ponctuation et les espaces) :
XGXYYXMETFXFXVHGYBZNKTMBHGWXYBZNKBGXLWTGLTGMXLTIITKNXTW
XNQKXIKBLXLXMJNXCTOTBLWXCTKXVHIBXXLXMKHNOTBMLNKETIHKMX
Tester tous les décalages est facile :
def testetout(chaine):
for i in range(1, 26):
print(i, cesar(chaine, -i))
Ce qui donne dans notre exemple :
1 WFWXXWLDSEWEWUGFXAYMJSLAGFVWXAYMJAFWKVSFKSFLWKSHHSJMWSVWMPJWHJAKWKWLIMWBSNSAKVWBSJWUGHAWWKWLJGMNSALKMJDSHGJLW
2 VEVWWVKCRDVDVTFEWZXLIRKZFEUVWZXLIZEVJUREJREKVJRGGRILVRUVLOIVGIZJVJVKHLVARMRZJUVARIVTFGZVVJVKIFLMRZKJLICRGFIKV
3 UDUVVUJBQCUCUSEDVYWKHQJYEDTUVYWKHYDUITQDIQDJUIQFFQHKUQTUKNHUFHYIUIUJGKUZQLQYITUZQHUSEFYUUIUJHEKLQYJIKHBQFEHJU
4 TCTUUTIAPBTBTRDCUXVJGPIXDCSTUXVJGXCTHSPCHPCITHPEEPGJTPSTJMGTEGXHTHTIFJTYPKPXHSTYPGTRDEXTTHTIGDJKPXIHJGAPEDGIT
5 SBSTTSHZOASASQCBTWUIFOHWCBRSTWUIFWBSGROBGOBHSGODDOFISORSILFSDFWGSGSHEISXOJOWGRSXOFSQCDWSSGSHFCIJOWHGIFZODCFHS
6 RARSSRGYNZRZRPBASVTHENGVBAQRSVTHEVARFQNAFNAGRFNCCNEHRNQRHKERCEVFRFRGDHRWNINVFQRWNERPBCVRRFRGEBHINVGFHEYNCBEGR
7 QZQRRQFXMYQYQOAZRUSGDMFUAZPQRUSGDUZQEPMZEMZFQEMBBMDGQMPQGJDQBDUEQEQFCGQVMHMUEPQVMDQOABUQQEQFDAGHMUFEGDXMBADFQ
8 PYPQQPEWLXPXPNZYQTRFCLETZYOPQTRFCTYPDOLYDLYEPDLAALCFPLOPFICPACTDPDPEBFPULGLTDOPULCPNZATPPDPECZFGLTEDFCWLAZCEP
9 OXOPPODVKWOWOMYXPSQEBKDSYXNOPSQEBSXOCNKXCKXDOCKZZKBEOKNOEHBOZBSCOCODAEOTKFKSCNOTKBOMYZSOOCODBYEFKSDCEBVKZYBDO
10 NWNOONCUJVNVNLXWORPDAJCRXWMNORPDARWNBMJWBJWCNBJYYJADNJMNDGANYARBNBNCZDNSJEJRBMNSJANLXYRNNBNCAXDEJRCBDAUJYXACN
11 MVMNNMBTIUMUMKWVNQOCZIBQWVLMNQOCZQVMALIVAIVBMAIXXIZCMILMCFZMXZQAMAMBYCMRIDIQALMRIZMKWXQMMAMBZWCDIQBACZTIXWZBM
12 LULMMLASHTLTLJVUMPNBYHAPVUKLMPNBYPULZKHUZHUALZHWWHYBLHKLBEYLWYPZLZLAXBLQHCHPZKLQHYLJVWPLLZLAYVBCHPAZBYSHWVYAL
13 KTKLLKZRGSKSKIUTLOMAXGZOUTJKLOMAXOTKYJGTYGTZKYGVVGXAKGJKADXKVXOYKYKZWAKPGBGOYJKPGXKIUVOKKYKZXUABGOZYAXRGVUXZK
14 JSJKKJYQFRJRJHTSKNLZWFYNTSIJKNLZWNSJXIFSXFSYJXFUUFWZJFIJZCWJUWNXJXJYVZJOFAFNXIJOFWJHTUNJJXJYWTZAFNYXZWQFUTWYJ
15 IRIJJIXPEQIQIGSRJMKYVEXMSRHIJMKYVMRIWHERWERXIWETTEVYIEHIYBVITVMWIWIXUYINEZEMWHINEVIGSTMIIWIXVSYZEMXWYVPETSVXI
16 HQHIIHWODPHPHFRQILJXUDWLRQGHILJXULQHVGDQVDQWHVDSSDUXHDGHXAUHSULVHVHWTXHMDYDLVGHMDUHFRSLHHVHWURXYDLWVXUODSRUWH
17 GPGHHGVNCOGOGEQPHKIWTCVKQPFGHKIWTKPGUFCPUCPVGUCRRCTWGCFGWZTGRTKUGUGVSWGLCXCKUFGLCTGEQRKGGUGVTQWXCKVUWTNCRQTVG
18 FOFGGFUMBNFNFDPOGJHVSBUJPOEFGJHVSJOFTEBOTBOUFTBQQBSVFBEFVYSFQSJTFTFURVFKBWBJTEFKBSFDPQJFFTFUSPVWBJUTVSMBQPSUF
19 ENEFFETLAMEMECONFIGURATIONDEFIGURINESDANSANTESAPPARUEADEUXREPRISESETQUEJAVAISDEJARECOPIEESETROUVAITSURLAPORTE
20 DMDEEDSKZLDLDBNMEHFTQZSHNMCDEHFTQHMDRCZMRZMSDRZOOZQTDZCDTWQDOQHRDRDSPTDIZUZHRCDIZQDBNOHDDRDSQNTUZHSRTQKZONQSD
21 CLCDDCRJYKCKCAMLDGESPYRGMLBCDGESPGLCQBYLQYLRCQYNNYPSCYBCSVPCNPGQCQCROSCHYTYGQBCHYPCAMNGCCQCRPMSTYGRQSPJYNMPRC
22 BKBCCBQIXJBJBZLKCFDROXQFLKABCFDROFKBPAXKPXKQBPXMMXORBXABRUOBMOFPBPBQNRBGXSXFPABGXOBZLMFBBPBQOLRSXFQPROIXMLOQB
23 AJABBAPHWIAIAYKJBECQNWPEKJZABECQNEJAOZWJOWJPAOWLLWNQAWZAQTNALNEOAOAPMQAFWRWEOZAFWNAYKLEAAOAPNKQRWEPOQNHWLKNPA
24 ZIZAAZOGVHZHZXJIADBPMVODJIYZADBPMDIZNYVINVIOZNVKKVMPZVYZPSMZKMDNZNZOLPZEVQVDNYZEVMZXJKDZZNZOMJPQVDONPMGVKJMOZ
25 YHYZZYNFUGYGYWIHZCAOLUNCIHXYZCAOLCHYMXUHMUHNYMUJJULOYUXYORLYJLCMYMYNKOYDUPUCMXYDULYWIJCYYMYNLIOPUCNMOLFUJILNY
On retrouve facilement le texte d’origine (décalage 19). Cette méthode n’est toutefois pas complètement automatique, car nous devons repérer le texte intelligible parmi les 26 testes proposés. Or, pour pouvoir utiliser ce système dans un cadre un peu plus complexe (celui du chiffre de Vigénère… ça vient…), il faut que la machine trouve le bon décalage toute seule.
Une façon d’y parvenir est de faire un pari statistique sur les fréquences d’apparition des lettres (méthode de l’analyse fréquentielle). Sachant que le texte est en français, nous pouvons supposer que le texte possède le nombre de A moyen d’un texte français, le nombre de B moyen, etc… Cela sera d’autant plus vrai que le texte à déchiffrer sera long.
La répartition des lettres en français est donnée par l’histogramme suivant :
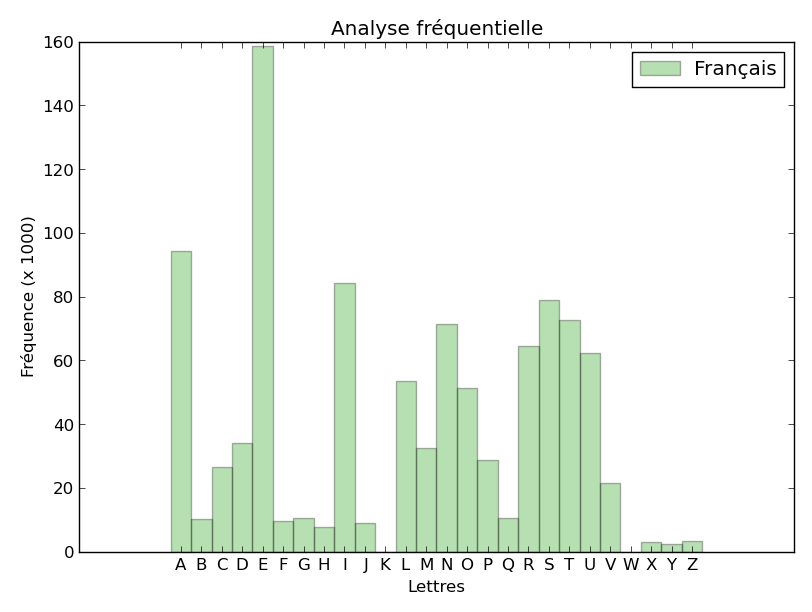
La lettre qui revient le plus souvent est le E, suivie par A, alors que les deux plus rares sont K et W.
Si nous prenons un texte crypté avec le chiffre de César, et un décalage inconnu, par exemple :
VUHHBZZPZLZSLAAYLZHBZLUHALAPSWHYHPALAYLSLWYLTPLYXB
PHPALJYPAZLZYHWWVYAZLUKPCPZHUASLZWHNLZHSHMHVUKBUTL
TVPYLAHUKPZXBHBWHYHCHUASLZJVUZBSZLASLZNLULYHBELJYP
CHPLUASLZSLBYZKHUZAVBALSLALUKBLKLZMLBPSSLZVUWVZZLK
LLUMPUKLJLZHYKLZSLAAYLZHJPJLYVULAZHJVYYLZWVUKHUJLH
CLJZLZHTPZZBYZLZHMMHPYLZKVTLZAPXBLZPSFLTWSVFHPAWVB
YSLZJOVZLZAVBAHMHPAZLJYLALZBULLZWLJLKLJOPMMYLXBPLU
YLUKHPASLZLUZPUPUALSSPNPISLSLZSLAAYLZLAHUAKPZWVZLL
ZKLTHUPLYLHULWVBCVPYQHTHPZMVYTLYBUTVALAXBPJVUZPZAH
PAQLSLKPZWVBYJLBEXBPCVBKYVUASLZKLJOPMMYLYHJOHUNLYS
LYHUNKLZSLAAYLZKHUZSHSWOHILALULJYPCHUASHXBHAYPLTLW
VBYSHWYLTPLYLJLZAHKPYLSLKWVBYSHLAHPUZPKLZBPAL
et que nous traçons l’histogramme des fréquences des lettres, nous obtenons :
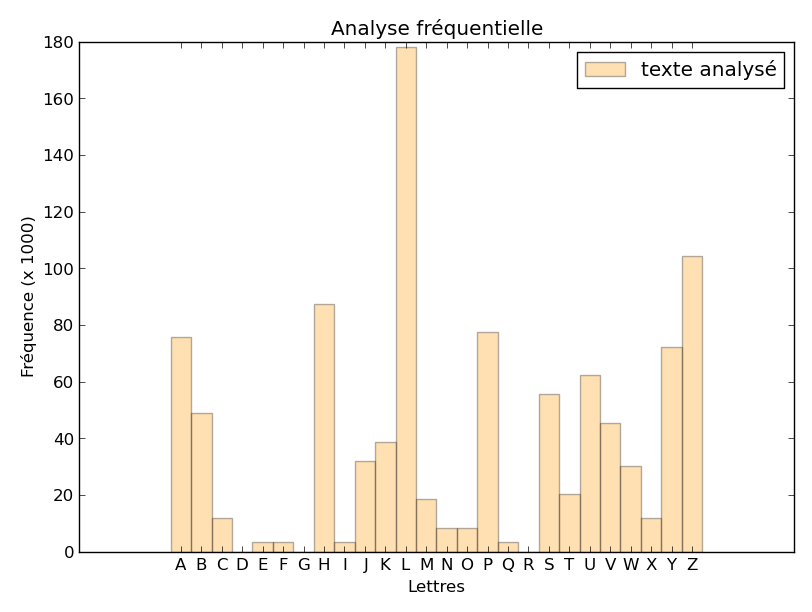
L’histogramme est presque le même que l’histogramme moyen du français (si, si, regardez bien…) mais décalé de
la valeur utilisée comme clé dans la méthode de chiffrement. On retrouve le pic maximum, ici en L,
suivi 6 lettres plus loin d’une valeur nulle.
Voici une fonction Python qui calcule les fréquences des lettres d’une chaîne de caractère :
def frequences(chaine):
freq = [0] * 26
for c in chaine:
if c in string.ascii_uppercase:
freq[ord(c) - ord('A')] += 1
somme=sum(freq)
freq=[v / somme * 1000.0 for v in freq]
return freq
Nous en sommes donc réduits à rechercher la valeur du décalage qui fait coïncider les deux histogrammes.
Voici quelques exemples d’histogrammes obtenus à partir du texte chiffré, sans décalage, avec un décalage de 1 (vers la droite pour le texte analysé), de 10 et de 19.
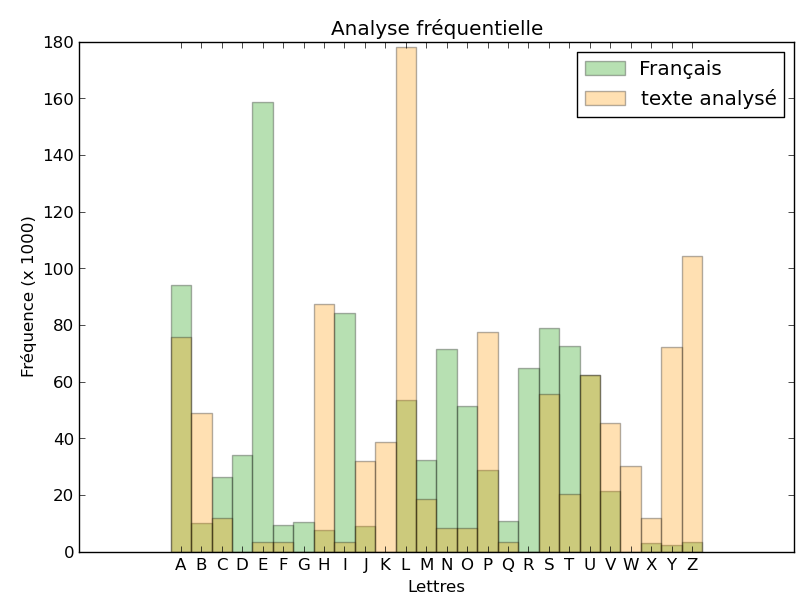
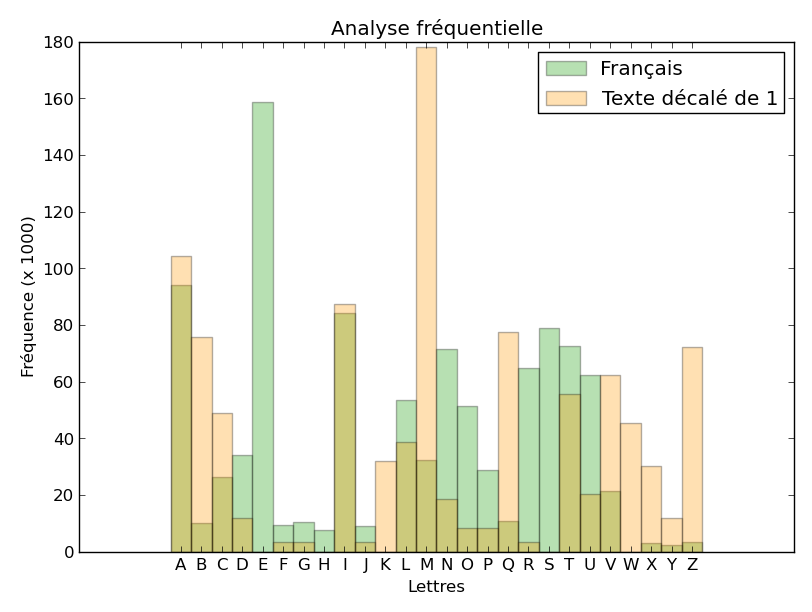
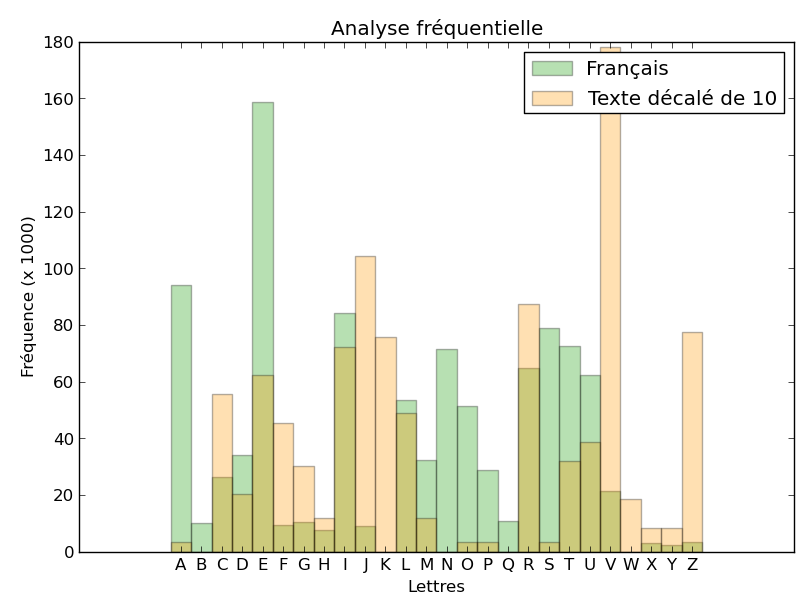
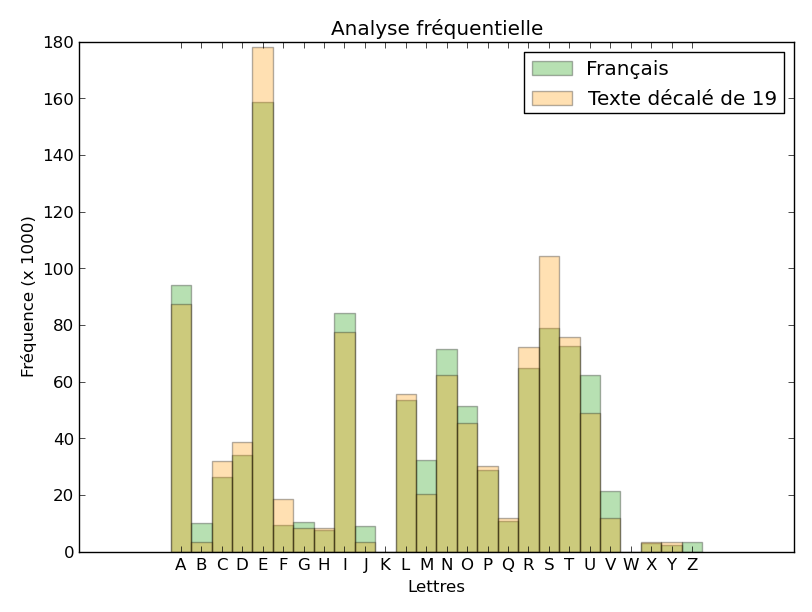
Le décalage de 19 semble faire coïncider assez bien les deux histogrammes. Nous pouvons retrouver ce résultat en calculant la corrélation entre les deux histogrammes. Pour chaque décalage (de 0 à 25), faisons la somme, pour les 26 lettres, du produit des 2 fréquences obtenues dans le texte chiffré décalé et en français moyen. Si nous représentons ces valeurs obtenues, en fonction du décalage (en abscisse), nous obtenons :
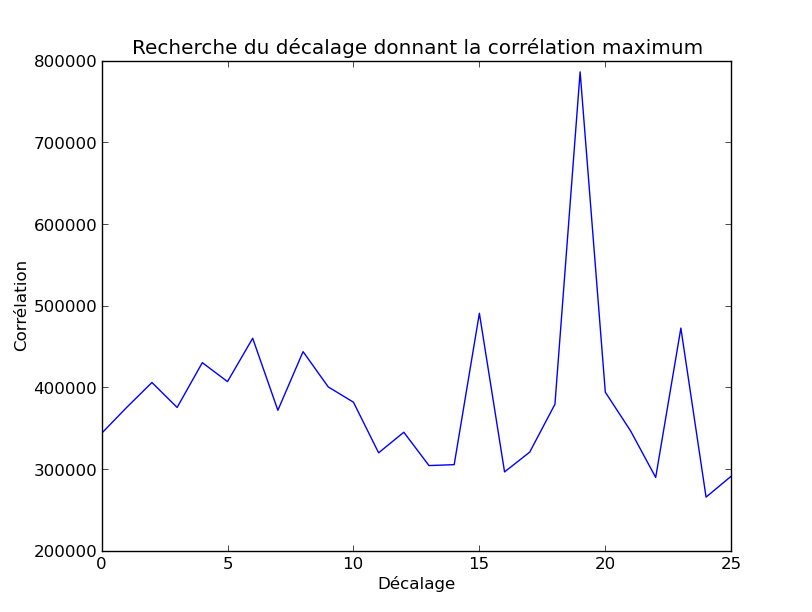
Le maximum est obtenu pour 19, le décalage correct. Nous disposons donc maintenant d’un moyen de déchiffrer automatiquement le chiffre de César :
- pour chacun des 26 décalages possibles (y compris 0) : calcul de la corrélation discrète des fréquences des lettres entre le texte chiffré décalé et le français moyen.
- recherche du maximum de corrélation obtenu, qui correspond au décalage utilisé dans le chiffrement.
Le code Python suivant fait ce travail. Il utilise les fréquences moyennes du français données sur Wikipédia
(Analyse fréquentielle),
ainsi que la fonction frequences que nous avons donnée précédemment.
def cherche_cle_cesar(chaine):
francais = [942, 102, 264, 339, 1587, 95, 104, 77, 841, 89, 0, 534, 324, 715, 514, 286, 106, 646, 790, 726, 624, 215, 0, 30, 24, 32]
corr = [0] * 26
for dec in range(26):
res = frequences(cesar(chaine, -dec))
corr[dec] = sum(a * b for a, b in zip(res,francais))
return corr.index(max(corr))
def autocesar(chaine):
cle = cherche_cle_cesar(chaine)
print("Clé : ",cle)
return cesar(chaine, -cle)
Testons sur le premier cryptogramme d’exemple, pourtant court :
>>> s = 'XGXYYXMETFXFXVHGYBZNKTMBHGWXYBZNKBGXLWTGLTGMXLTIITKNXTWXNQKXIKBLXLXMJNXCTOTBLWXCTKXVHIBXXLXMKHNOTBMLNKETIHKMX'
>>> print(autocesar(s))
Clé : 19
ENEFFETLAMEMECONFIGURATIONDEFIGURINESDANSANTESAPPARUEADEUXREPRISESETQUEJAVAISDEJARECOPIEESETROUVAITSURLAPORTE
Nous trouvons directement le message en clair, ainsi que la valeur du décalage qui avait été utilisée pour chiffrer.
Chiffre de Vigénère
Au 16e siècle, Blaise de Vigénère publie une méthode de chiffrement, basée sur le carré de Trithème. Il l’aurait repris à son compte alors qu’elle aurait été initialement publiée par Giovan Battista Bellaso et peut-être par Giambattista della Porta.
Pour utiliser la méthode de Vigénère, nous devons au préalable choisir un mot clé. Par exemple MARS. Puis, nous écrivons le texte en clair en faisant correspondre chacune des lettres avec une lettre du mot clé (en répétant celui-ci plusieurs fois) :
LESOLEILARENDEZVOUSAVECLALUNE
MARSMARSMARSMARSMARSMARSMARSM
Puis, pour chaque couple de lettres clair/clé, nous regardons dans le tableau suivant la ligne correspondant à la clé et la colonne correspondant au texte clair. À l’intersection se trouve la lettre chiffrée, que nous reportons sous le mot clé. Dans l’exemple qui précède, on commence par regarder ligne M et colonne L, pour trouver un X, qui sera la première lettre du cryptogramme.
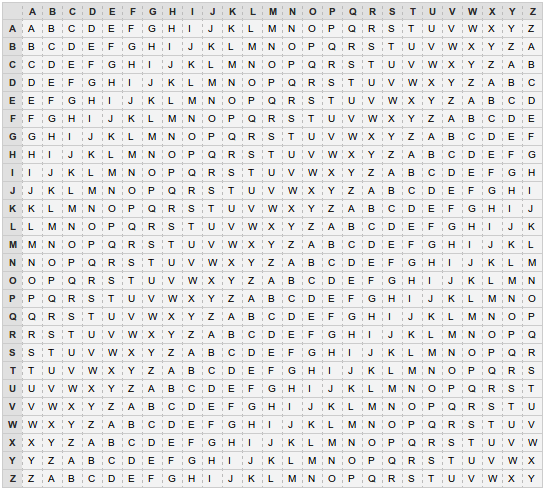
Voici ce que que nous obtenons, dans le cas de notre exemple :
LESOLEILARENDEZVOUSAVECLALUNE
MARSMARSMARSMARSMARSMARSMARSM
XEJGXEZDMRVFPEQNAUJSHETDMLLFQ
Cette méthode de chiffrement est dite polyalphabétique, contrairement au chiffre de César qui est monoalphabétique. En effet, la lettre O de SOLEIL est changée en G alors que la lettre O de VOUS est changée en A. Avec le chiffre de César, chaque lettre est toujours changée en la même lettre chiffrée.
Le gros avantage de cette méthode par rapport au chiffre de César (pour celui qui chiffre) est que l’analyse fréquentielle ne semble plus rien donner… Voyons ce que nous obtenons pour le texte chiffré suivant, relativement long (présenté par paquets de 4 lettres) :
BONR OWRX CUIE TFSY ENRV XCAI XIAS YWYI ALVX GCII XYAX WUSI
FCYP PMHV WUDY PFYI UYII YUVW OYPV TLRI ECYP PRNQ THNP ZHTX
PGCW LPRG LNGI YNVS YKHI DNPI BORG PFNZ POGH TLRV PJRX LCGM
WGNG SCAE WYZI YNFY CFUS YHRY CDRR LOEE TMCY WYYY TUCT CYAH
CYQE TFYI FLFM WHRQ THGI CLBK PUCE DYGM WWBR ECAY LXRW PJNV
WYEE WOVQ PGRG PMGG PKHI YIHW LJCI WIAW FHPV JJGS RLNQ XYQM
DUVX TFQE YMYI BORP WYFI YMRW EWNG SYFS FMQI DFRX ELRW MLBY
TFYI PMNH PMFI THRX BOVG ZHII YUOP PGRR EXVW AIFI PMSS CGRV
LCRR EOAI ABEE DYVR EYYP TAVF WYDY LHQN PJRR DYDY TFLE WUCI
FNRX CYYI IJYM NUGM ZHBY WCAH TWNX TIAH FHRK CUAH PXRG ZOII
CNRT ZOEQ ZHPS XJGI UYCI YMNM DKHM WHLE GUVX LVFS WOZI YNEM
PHZE TMWI RUEH LCCV FXRQ XYAX XIAS ACAM ZHYI ALBJ PMFI FLCV
TNNP ZLFP PFVZ CYRX WYCE CWUI XCAI EFRW NIZT LLNX ZOFP PMQI
FRPI DXRY IYPV TNHV PMAI DIAX AUFH PFNQ PGRQ LCAH TNVP WYPV
JJGS RLNQ XYRW EJBW EYEM POEE FFVZ CYRX UYAZ ZCFY YYCV POII
TLEI QLNK LVYI PHRJ QYGP LJEI XCRV PFRX ELRI DNHR PXBY MFRQ
BOBR NBRV NBRV LCGZ LCAI XYAX OUAW WYYM GLRH PNHV WYFS YWNV
PFYI YYSY EUWS FNRI LFNP ABNF PNVW WUAH LCFU FUHB TPRW TYPP
PUVR DCQS YWVP JUNY XIVR DXRY IWRR EMNR DYAX CYYI XUAY DWEM
EYGP PXBG FGRR EWRP LDRR NIAZ TYAW XYCE COGE DMRD WITM BORN
PMHM DXBR NWBR OOVX LJRR DYEV PJEM EGBR ZHPP PKHI WOAH PMCS
DMRW DYHV DXRG PFVZ CYNY CUGV LWRG PMPE CUPX PLRW XSFX PLVI
FRZE TMDY TXVE MFRI EUVX NYCS DMRW DYHV YUHV LCGM WJBM YNZM
DMBR YIZI YKHI WKHI PHQV ZCGI YWRQ LHHW NLVX XIAS YWYI CYYI
GUFI DFHR PNGI DJEM EOAI QIEX PFBY AYRX AUFW LMBM RHRY DYZI
YNRR CYIY PFRW ALRQ TYEI DJNK PMQY WCIV PUHZ PLFS OYYE DYPS
YXRG PFYI OOSE FRGM ELRM WXRG ZOIV TNHR PMBV EYQI XUPY WYDY
TZNM DUVX LFBI TFYI QZRX OOAI EUPL PXRR NLRG PJRR OUAX PHLV
PANV OUAX OYCV PMBR OCFX THTY LCGU FYYU FYFG LLNG EYEI DUQI
XCRJ QUPI DGBR ZHPP PWBQ ALVX BORP LYGE TNYI AIVR ECAX PLRW
DUAX TFFE NBNV YUQS YWFY CFNQ LWHP PYGW LAES DMRP ZOCI LCQE
YNVP QCAM EJNV CYPS YHNM ELRP PMFM RHRW BORZ ZCPM NUEE NNRV
PMEY YCDY PKHM WFHX DUAW SYFM EYEE CHRW LEAY DMRQ XMRG CCNX
TFQY YNBR ELVS XJUE YNZE TMPI DNHR YIZG PFNI EOAR ZGVW WUAH
LCFI YWBV PWRP FCQY YMNZ LHGH FRIM PMQY YUYG SCZM DNRG PFRF
CY
Nous trouvons cette répartition de fréquences :
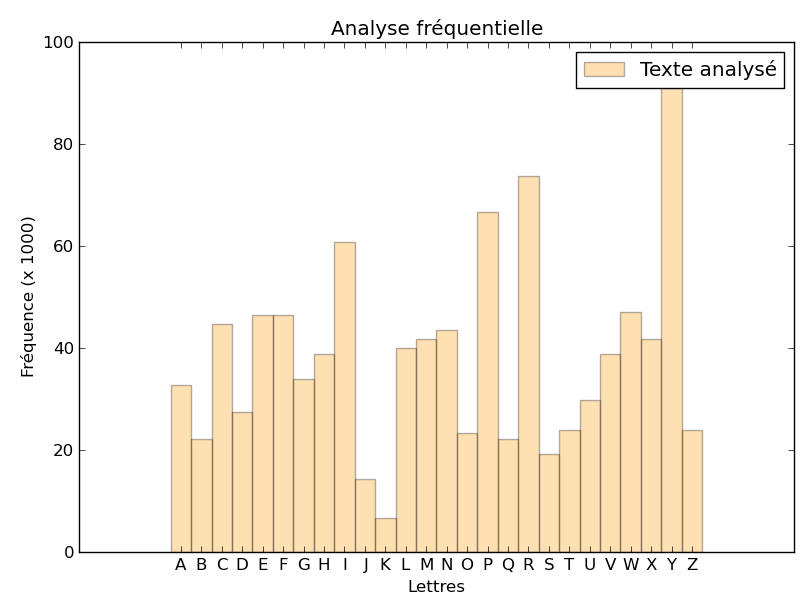
Analyse fréquentielle d'un texte chiffré avec la méthode de Vigénère
On a bien une sorte de pic sur le Y, mais l’histogramme ne correspond toutefois plus
à celui, caractéristique, du français. Il a été en quelque sorte «lissé».
Sous-textes
Supposons cependant que nous ayons deviné que la clé a pour longueur 4.
Dans notre exemple court, nous allons sélectionner uniquement les lettres
du texte clair qui «tombent» en face de la lettre M de la clé :
LLADOVAE
MMMMMMMM
XXMPAHMQ
Sur ce sous-texte, la substitution est monoalphabétique.
Le L est changé, les deux fois, en X
et le A est toujours changé en M. De plus
cette substitution est un décalage de 12 (lettre M de la clé).
Voyons ce que donne notre texte chiffré long si nous ne sélectionnons qu’une lettre sur 4, en commençant par la première (ce qui revient à ne conserver ici que la première lettre de chaque paquet de 4 lettres du message chiffré complet) :
BOCTEXXYAGXWFPWPUYOTEPTZPLLYYDBPPTPLWSWYCYCLTWTC
CTFWTCPDWELPWWPPPYLWFJRXDTYBWYESFDEMTPPTBZYPEAPC
LEADETWLPDTWFCINZWTTFCPZCZZXUYDWGLWYPTRLFXXAZAPF
TZPCWCXENLZPFDITPDAPPLTWJRXEEPFCUZYPTQLPQLXPEDPM
BNNLLXOWGPWYPYEFLAPWLFTTPDYJXDIEDCXDEPFELNTXCDWB
PDNOLDPEZPWPDDDPCCLPCPXPFTTMENDDYLWYDYYWPZYLNXYC
GDPDEQPAALRDYCPATDPWPPODYPOFEWZTPEXWTDLTQOEPNPOP
POOPOTLFFLEDXQDZPABLTAEPDTNYYCLPLDZLYQECYEPRBZNN
PYPWDSECLDXCTYEXYTDYPEZWLYPFYLFPYSDPC
Traçons l’histogramme des fréquences d’apparition en utilisant uniquement ce sous-texte :
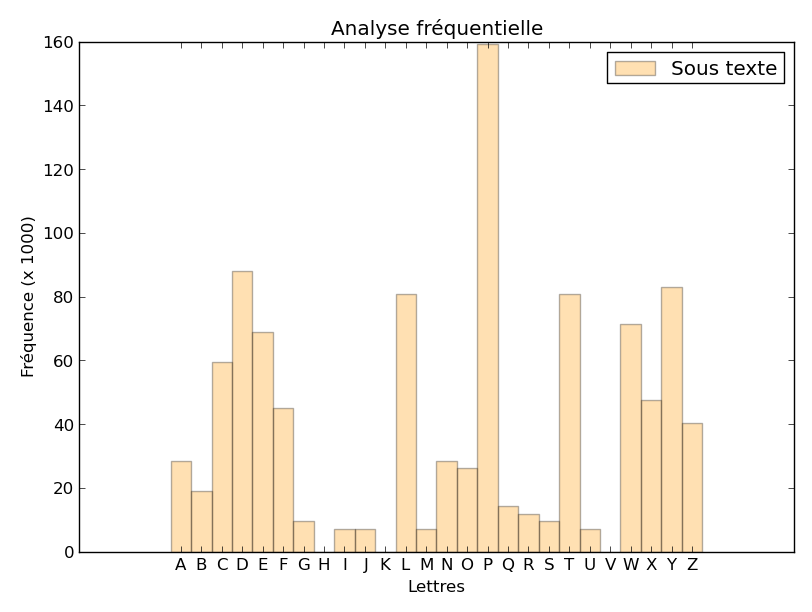
Analyse fréquentielle d'un sous texte (une lettre sur 4)
Cette fois, nous retrouvons l’histogramme caractéristique du français mais avec un décalage (qui semble valoir ici 11 si on se fie à la position du maximum). C’est finalement bien compréhensible, car la fréquence d’apparition d’une lettre donnée, par exemple le E, ne varie pas en fonction de sa position dans le texte. Elle varie certainement en fonction de la position dans le mot (je n’ai pas vérifié, mais il est probable que le E apparaisse plus souvent en fin de mot qu’en avant dernière lettre d’un mot par exemple), mais comme la longueur des mots varie, et qu’on les met tous bout à bout…
L’obtention d’un diagramme des fréquences qui ressemble (décalé) à celui du Français en ne prenant qu’une lettre sur 4 nous indique que la clé utilisée avait sans doute une longueur 4 (ou un diviseur de 4… par exemple 2) car nous savons que le sous-texte a été chiffré par une substitution monoalphabétique (qui de plus est un simple décalage), c’est à dire toujours avec la même lettre de la clé.
Nous pouvons réutiliser le travail réalisé sur le déchiffrement automatique de César et l’appliquer à notre sous-texte afin de déterminer le décalage utilisé, et donc la lettre de la clé correspondante (A pour un décalage de 0, B pour un décalage de 1 etc…) :
# Entrer tout le texte, sans aucun caractère parasite
>>> t="""BONROWRXCUIETFSYENRVXCAIXIASYWYIALVXGCIIXYAXWUSIFCYPPMHV..."""
>>> cherche_cle_cesar(t[0::4])
11
Nous voyons que le décalage utilisé était 11, ce qui correspond à la lettre L dans le carré de Trithème. La première lettre de la clé est donc L.
Nous pouvons ensuite faire de même pour les 3 autres sous-textes, obtenus en ne prenant qu’une lettre sur 4, mais en commençant sur la 2ème, puis la 3ème et enfin la 4ème lettre du cryptogramme complet. C’est de cette manière que la fonction suivante trouve le mot de passe utilisé, à condition qu’on connaisse au préalable sa longueur.
def cherche_cle_vigenere(chaine, n) :
return "".join( chr(ord('A') + cherche_cle_cesar(chaine[i::n])) for i in range(n))
En testant sur l’exemple fourni :
>>> cherche_cle_vigenere(t, 4)
'LUNE'
Il reste que nous avons dû deviner que la longueur de la clé était 4. Y a-t-il un moyen de le calculer ?
Indice de coïncidence
Une première méthode pour déduire la longueur de la clé a été proposée par Charles Babbage (le concepteur de la Machine analytique sur laquelle Ada, comptesse de Lovelace a inventé le métier de programmeur) au milieu du 19e siècle. Cette méthode consiste à trouver des groupes de lettres qui se suivent et qui se répètent dans le texte. Il faut un texte assez long, et c’est assez hasardeux (mais faisable à la main).
Plus tard, entre les deux guerres, William Friedman
a «inventé» l'indice de coïncidence,
qui mesure la probabilité que, prenant deux lettres au hasard dans un texte, ce soit les mêmes.
Cet indice se calcule ainsi : $IC = \sum_{q=A}^{q=Z}\frac{n_{q}(n_{q}-1)}{n(n-1)}$
def indice_coincidence(chaine):
app = apparitions(chaine)
s = sum (n * (n - 1) for n in app)
somme = sum(app)
return s / (somme * (somme - 1))
Dans le code qui précède, apparitions(chaine) renvoie une liste contenant le nombre de ‘A', le nombre de ‘B' etc… Cette fonction ressemble beaucoup à la fonction frequences que nous avons déjà vue. Nous pourrions par exemple la coder ainsi :
def apparitions(chaine):
app = [0] * 26
for c in chaine :
if c in string.ascii_uppercase:
app[ord(c) - ord('A')] += 1
return app
L’indice de coïncidence a une propriété qui va beaucoup nous intéresser : il est invariant par toute substitution monoalphabétique. En particulier, si on utilise un simple décalage (chiffre de César), les valeurs des nq sont échangés entre elles, mais tous les termes se retrouvent dans le calcul, avant ou après substitution, et la somme étant commutative, le résultat est inchangé. Par exemple, pour un décalage de 3, le nombre de A devient le nombre de D, le nombre de B devient le nombre de E… le nombre de X devient le nombre de A etc.
Sur notre exemple du début (César) , nous pouvons calculer l’indice du texte en clair :
>>> indice_coincidence('ENEFFETLAMEMECONFIGURATIONDEFIGURINESDANSANTESAPPARUEADEUXREPRISESETQUEJAVAISDEJARECOPIEESETROUVAITSURLAPORTE')
0.07526333673122663
Puis l’indice du même texte, chiffré
>>> indice_coincidence('XGXYYXMETFXFXVHGYBZNKTMBHGWXYBZNKBGXLWTGLTGMXLTIITKNXTWXNQKXIKBLXLXMJNXCTOTBLWXCTKXVHIBXXLXMKHNOTBMLNKETIHKMX')
0.07526333673122663
Ce sont exactement les mêmes, et ils sont à peu près égal à l’indice de coïncidence moyen constaté en français (donné égal à 0.0778 sur Wikipédia).
Voyons maintenant ce que donnerait cet indice sur une séquence de lettres prise au hasard. Il y aurait dans ce cas, si la séquence est assez longue, autant de A, que de B, etc… Dans un message de longueur n, chaque lettre apparaîtrait donc n/26 fois et l’indice vaudrait : $IC=\frac{1}{n(n-1)}\sum \frac{n}{26}(\frac{n}{26}-1) = (\frac{n}{26}-1)/(n-1)$.
Lorsque n est grand, cette valeur s’approche de $\frac{1}{26} \approx 0.385$.
Or, utiliser le chiffrement de Vigénère avec un clé un peu longue consiste justement à «randomiser» le texte chiffré, puisqu’on réalise, au niveau des fréquences d’apparition des lettres, la moyenne entre plusieurs histogrammes de fréquences (un pour chaque lettre de la clé).
Dans un premier temps, nous pouvons donc détecter, en calculant l’indice de coïncidence, si le texte est une substitution monoalphabétique (on trouvera l’indice du français, soit environ 0.07) ou une substitution polyalphabétique (on trouvera une valeur plus petite).
Voyons ce qu’on peut dire du texte suivant :
SORHZIROWPQXJSPTHICGSBAISORHHSJGPTGGPGHT
QVXHYGSWTQVTHIAOTGSQXSVTEYTGXXCRPJMSSVRS
WIZEAORVIISIGWWJUFIROVASWEFMCQMESWSSWDZY
IWSCDEGHMRIPXSVTAICHUJORSWPHOKXHHTGGWWJU
FIHZIHDPJGWXATASWSSTTBHTBXSIKTBMTRIRVEFI
IXRMDAITHTTIZTBXTHVTASSWJXSWTBKTBIGOPXZR
NOTPGHPIXGSQDMICEYTRIHGENSVHIGRSWHWZTAIC
HICGISWVXUIPBXHIMKORIZIHDVDPEQWPXHIHHSJH
IHZIHZECUYTGUJWZDIWHCRIQSCBYTGNJGUJOGTEY
TJSJGENSDIFSJJIAOFDBRTAEXGHPBWASGWWJUFIF
IMCCYHCGRITTHSJHISWJUWGJZXTOGTHIVOVSSXPW
XGSWDZYTDEGZEHWKCOXJFIASVTPYHGYGZIBCXZWH
SBIHHTDGWXPPTEYTRECGPPZECUYTORVZEXGIHORH
QIIHIRWVRCRHHECQIYOYGOMHQSBAICQIBSWTGWPW
WEOVASWEOKCCPTHPTTVPBEXGGDAQTSXPBXASWAOR
VIIHRECGPTGUJSPASWJBTXFEISHTGQTFWTGTPURD
ZIHOYGOMIRYASTAIWCOXJFIAZIBSRISRUSVBSVJB
WTQVTHHTQIIHICOXJFIBOMHRECGPTQEHOGIIIAXI
EFIHIQPWUJSPTQVNDXDUVPAQTSXPWXPBKAOMH
Faisons la chose suivante :
- calculons l’indice de coïncidence du texte (I1),
- puis la moyenne des 2 indices correspondant aux 2 sous textes obtenus en ne prenant qu’une lettre sur 2 et en commençant sur la première puis la deuxième lettre (I2),
- puis la moyenne des 3 indices correspondant aux 3 sous textes obtenus en ne prenant qu’une lettre sur 3 et en commençant sur la première, puis deuxième, puis troisième lettre (I3)
- … et ainsi de suite jusqu’à I12.
Voici les valeurs de ces indices, reportées sur un graphe :
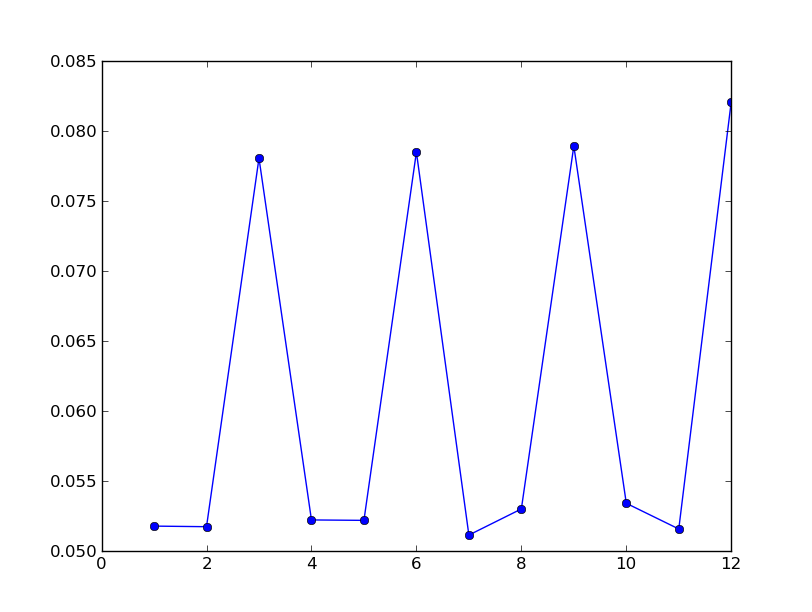
Le résultat est sans appel. Nous trouvons un indice proche de celui du français pour I3, I6, I9 et I12. Nous en déduisons que la clé est de longueur 3 (ou de longueur 6, si on la recopie 2 fois, de longueur 9 si on la recopie 3 fois…).
L’indice de coïncidence nous permet donc de trouver la longueur de la clé en recherchant les valeurs maximum de l’indice de coïncidence pour des sous-textes du texte chiffré. Une fois cette longueur connue, pour chaque sous-texte (il y en a autant qu’il y a de lettres dans la clé), nous pouvons retrouver la valeur de décalage (la lettre de la clé) utilisée et en déduire le texte en clair par des moyens que nous avons déjà vus.
Automatisation
Pour automatiser le tout, il suffit donc de rechercher parmi les indices de coïncidence calculés (en se limitant par exemple aux clés de longueur inférieure ou égale à 12), le premier qui est supérieur à un certain seuil (on peut fixer arbitrairement ce seuil à 0.068). Une fois cet indice connu, on en déduit la longueur de la clé, et on utilise ce qui a été vu précédemment :
def liste_indices(chaine, n):
res=[0]
for i in range(1, n + 1):
res.append(sum(indice_coincidence(chaine[k::i]) for k in range(i)))
res[-1] /= i
return res
def cherche_longueur_cle(chaine, seuil=0.068, nmax=12):
p = [(lcle, i) for lcle, i in enumerate(liste_indices(chaine, nmax)) if i > seuil]
return min(p)
Dans le cas de notre dernier exemple :
# Mettre tout le texte sans aucun caractère parasite
>>> u="SORHZIROWPQXJSPTHICGSBAISORHHSJGPTGGPGHT..."
>>> cherche_longueur_cle(u)
(3, 0.07804034921651412)
>>> cherche_cle_vigenere(u, 3)
'POE'
Le mot de passe est retrouvé, et il ne reste plus qu’à déchiffrer le texte, par exemple avec la fonction suivante :
def dechiffre_vigenere(s,cle):
l = []
for i, c in enumerate(s):
if c in string.ascii_uppercase:
c = ord(c) - ord(cle[i % len(cle)])
c = chr(c % 26 + ord('A'))
l.append(c)
return "".join(l)
Nous obtenons :
>>> dechiffre_vigenere(u, "POE")
'DANSLECASACTUELETENSOMMEDANSTOUSLESCASDECRITURESECRETE...
Le tout peut être lancé par une seule procédure :
def vigenere_automatique(chaine):
lgcle, indice = cherche_longueur_cle(chaine)
cle = cherche_cle_vigenere(chaine, lgcle)
return dechiffre_vigenere(chaine, cle)
