Le jeu Babylone™ est distribué par Descartes. Le principe du jeu est élémentaire, et peut être reproduit, par exemple, avec des briques de Légos™.
Règles
Le jeu se joue à deux joueurs. Le plateau de jeu est constitué de piles de briques de différentes couleurs. Dans une configuration initiale habituelle, chaque pile ne contient qu’une seule brique (mais on peut très bien démarrer dans une configuration différente). Le nombre de couleurs peut varier. Voici un exemple avec trois couleurs et deux briques de chaque couleur.

Exemples de briquettes pour jouer à Babylone
Chaque joueur joue à tour de rôle. À son tour, un joueur doit fusionner exactement deux piles en les posant l’une sur l’autre. Il ne peut le faire que si les deux piles sont composées du même nombre de briques ou si les briques supérieures de chaque pile sont de la même couleur. Si un joueur ne peut pas jouer il perd.
Voici un exemple de partie dans laquelle le joueur qui commence gagne (si vous avez imprimé ce billet… vous ne verrez rien…8-)
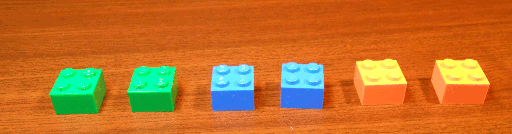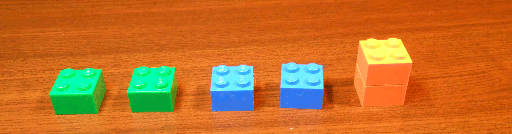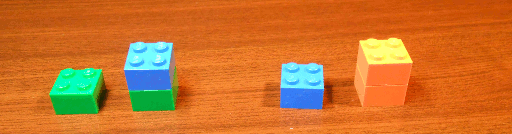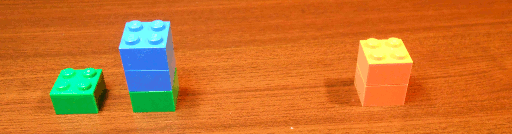
Le joueur qui commence gagne
Et un exemple de partie où il perd :

Le joueur qui commence perd
Ce jeu est donc un jeu de duel (il se joue à deux), dont l’issue est nécessairement la victoire d’un des deux joueurs (il y a une pile de moins à chaque tour, donc s’il y a n piles au début, au maximum n coups seront joués). Le hasard n’intervient pas, et c’est un jeu à information complète (chaque joueur connaît parfaitement et complètement la situation de l’autre). Il appartient à la catégorie des jeux de Nim (comme le jeu de Marienbad ou le jeu des allumettes, épreuve d’une célèbre émission télévisée).
Les jeux de Nim disposent nécessairement d’une stratégie optimale. Selon la configuration initiale, un des deux joueurs (celui qui commence, qu’on appellera le joueur 1, ou l’autre) dispose nécessairement d’une stratégie qui lui assure la victoire.
Graphe des configurations
Nous allons commencer par une configuration de départ simple, ne comportant que 4 piles d’une seule brique : deux piles jaunes et deux piles bleues. Supposons que nous ayons la main et commencions à jouer. Nous avons le choix entre 4 coups différents :
- empiler les deux briques jaunes
- empiler les deux briques bleues
- empiler une brique bleue sur une brique jaune
- empiler une brique jaune sur une brique bleue
Il est clair que les deux briques bleues jouent le même rôle (de même que les deux briques jaunes) et que l’ordre des piles n’a pas d’importance dans le jeu. En conséquence, ces quatre choix peuvent être représentés de la manière suivante :
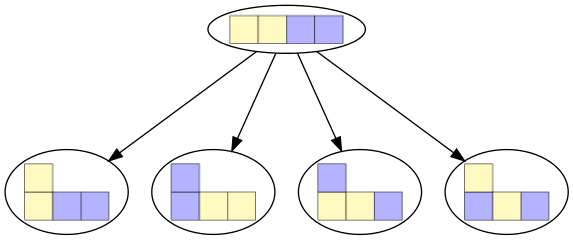
Figure 1
C’est maintenant au tour du joueur 2. Si le joueur 1 a empilé les deux briques bleues, la seule possibilité du joueur 2 est d’empiler les 2 briques jaunes. Si le joueur 1 a empilé la brique bleue sur la brique jaune, le joueur 2 peut :
- empiler les deux autre briques (dans un sens ou dans l’autre, laissant apparaître sur le dessus du bleu ou du jaune) ;
- empiler la brique bleue seule sur la pile faite par le joueur 1 ;
- empiler la pile faite par le joueur 1 sur la brique bleue seule.
Voici, pour chaque possibilité du joueur 1, la liste des possibilités qui s’offrent au joueur 2.
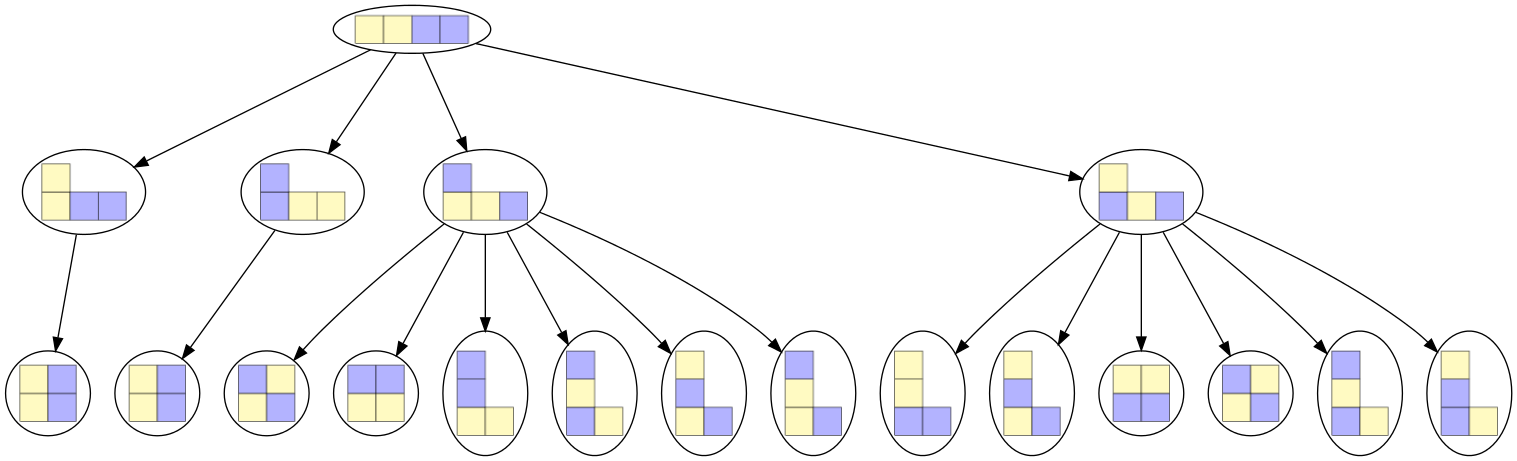
Figure 2
Remarquons que, pour réduire la taille du graphe, on peut identifier les deux nœuds, situés en bas à gauche du graphe, et dire que les deux configurations
 ou
ou
 mènent toutes les deux à la même configuration
mènent toutes les deux à la même configuration
 .
En «fusionnant» ainsi certains des nœuds les plus bas, nous obtenons ce nouveau graphe :
.
En «fusionnant» ainsi certains des nœuds les plus bas, nous obtenons ce nouveau graphe :
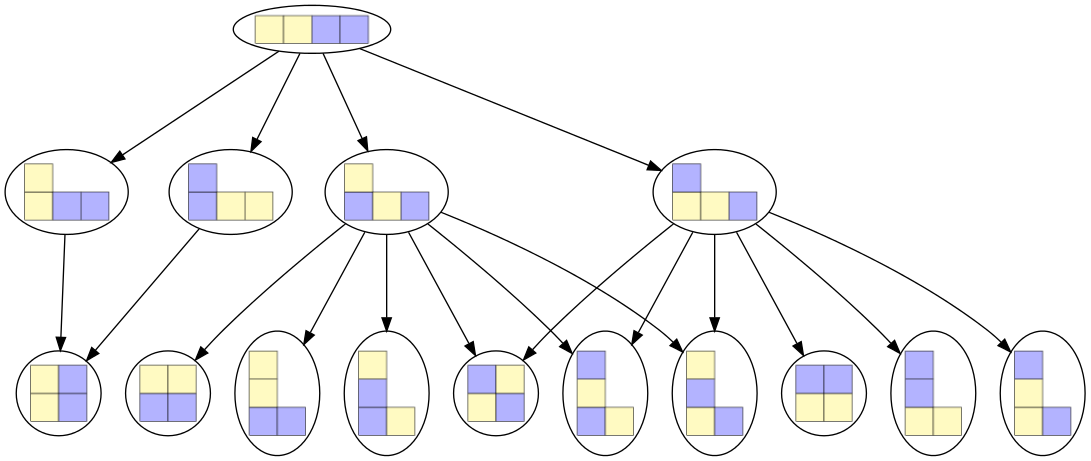
Figure 3
C’est maintenant au tour du joueur 1. Pour chacune des 10 situations dans lesquelles il peut se trouver, il a éventuellement plusieurs choix. Nous ajoutons donc un étage à notre graphe :
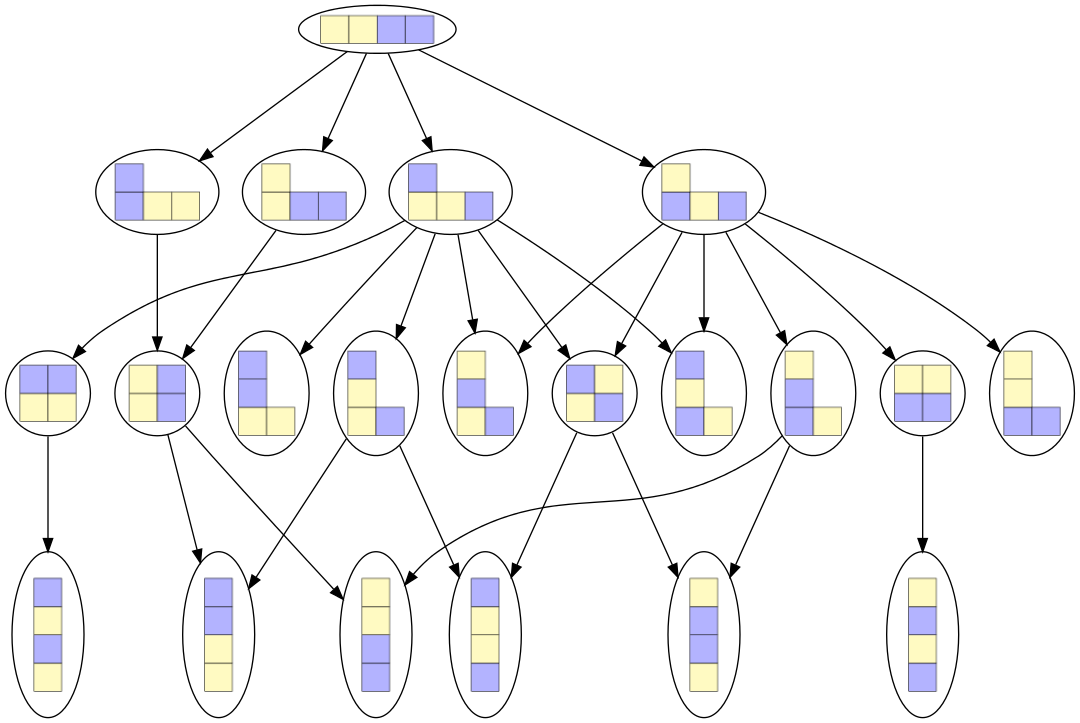
Figure 4
Algorithme du Minimax
Le graphe précédent contient donc toutes les parties possibles en démarrant dans la configuration 4 briques de 2 couleurs. Les configurations finales (les nœuds qui n’ont pas de successeur, c’est à dire pas de flèche sortantes) sont les configurations perdantes pour celui qui s’y trouve : on ne peut plus jouer, donc on perd.
Remarquons aussi que chaque étage du graphe correspond à un joueur particulier. Le joueur 1 est celui qui commence, puis le joueur 2 peut fait face à une des 4 configurations du second étage, puis à nouveau le joueur 1, dans une des 10 configurations de l’étage 3…
Si nous sommes le joueur 1 (celui qui commence) et que nous voulons gagner (ce qui est naturel…), alors les nœuds qui n’ont pas de successeurs sont gagnants pour nous s’ils sont sur un étage pair (car c’est alors au joueur 2 de jouer) et perdants pour nous s’ils sont sur un étage impair (car c’est à nous de jouer).
Colorons en vert ces nœuds gagnants et en rouge ces nœuds perdants. Nous obtenons ce graphe :
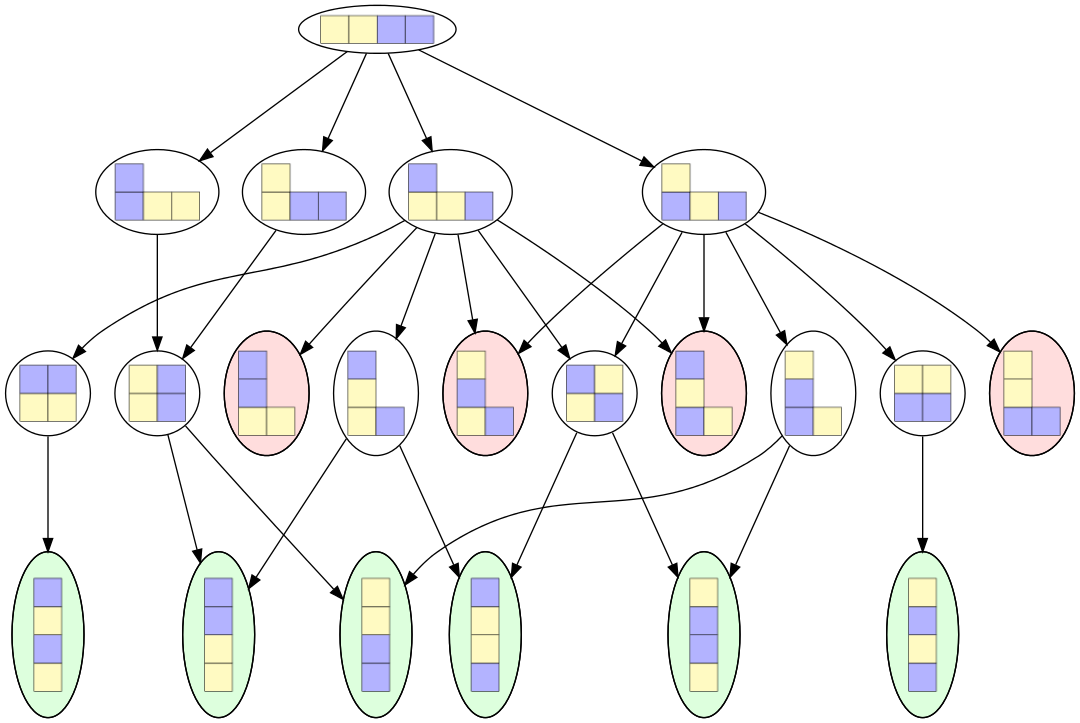
Figure 5
Continuons à colorier le graphe. Sur l’étage 3 (c’est à nous de jouer), certains nœuds de sont pas coloriés. Chacun de ces nœud a un successeur vert (une configuration gagnant pour nous). En conséquence ces nœuds, non encore coloriés peuvent être coloriés en vert car ils ont au moins un successeur vert, et que c’est ce coup que nous jouerons (pour gagner). Nous obtenons ainsi ce graphe :
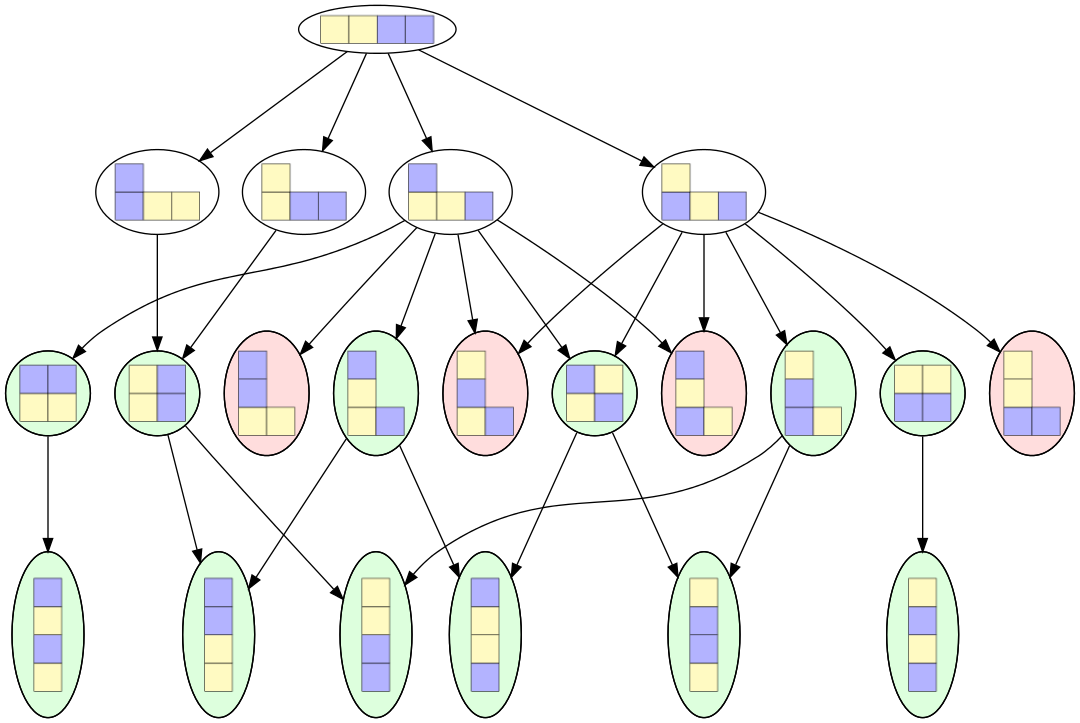
Figure 6
Essayons de colorier le second étage du graphe. À cet étage c’est au joueur 2 de jouer. S’il se trouve dans la configuration
 ,
il n’y a qu’un successeur, qui est gagnant pour le joueur 1. Ce nœud est donc perdant pour le joueur 2 et gagnant pour le joueur 1.
En effet, le joueur 2 n’a pas d’autre choix que de jouer de
,
il n’y a qu’un successeur, qui est gagnant pour le joueur 1. Ce nœud est donc perdant pour le joueur 2 et gagnant pour le joueur 1.
En effet, le joueur 2 n’a pas d’autre choix que de jouer de
 vers
vers
 qui est une configuration perdante pour lui.
C’est la même chose pour le second nœud du même étage. Ces deux nœuds seront donc verts. Pour les nœuds
qui est une configuration perdante pour lui.
C’est la même chose pour le second nœud du même étage. Ces deux nœuds seront donc verts. Pour les nœuds
 et
et  ,
certains successeurs sont verts et d’autres rouges.
Le joueur 2, qui joue de manière optimale peut donc aller sur un nœud rouge,
gagnant pour lui. En conséquence,
les nœuds
,
certains successeurs sont verts et d’autres rouges.
Le joueur 2, qui joue de manière optimale peut donc aller sur un nœud rouge,
gagnant pour lui. En conséquence,
les nœuds  et
et  sont gagnants pour le joueur 2. Il seront donc colorés en rouge.
sont gagnants pour le joueur 2. Il seront donc colorés en rouge.
Nous obtenons ce graphe :
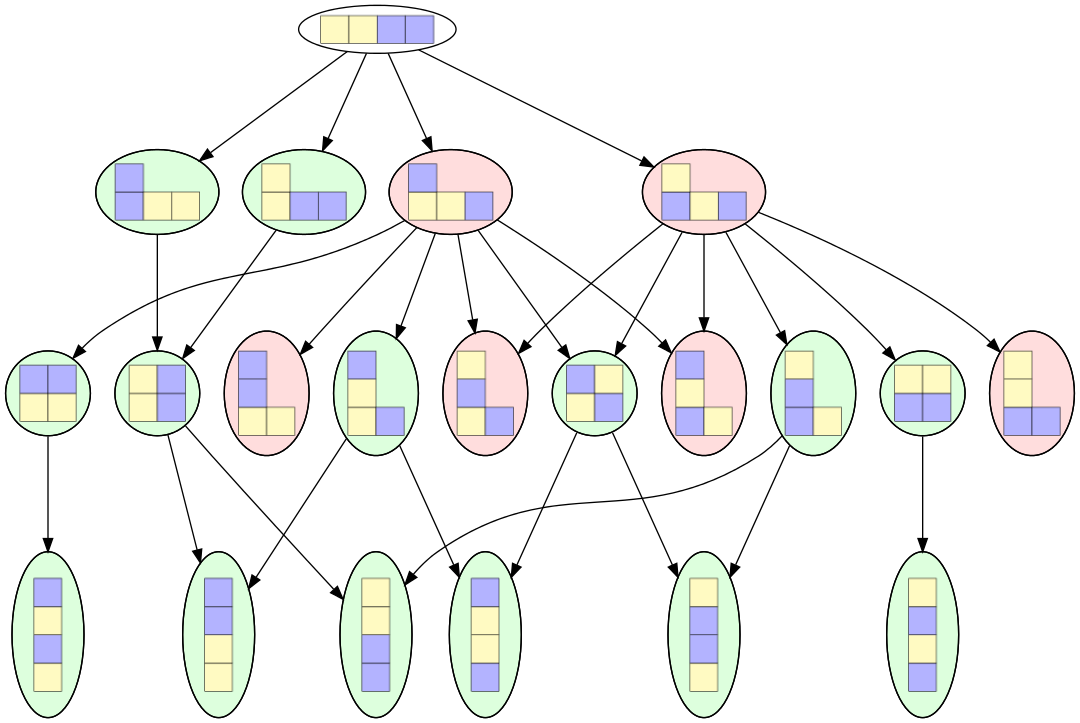
Figure 7
Nous pouvons maintenant colorer le nœud de départ. C’est au tour du joueur 1 qui a 4 choix. Deux choix mènent à une configuration rouge, certainement perdante pour le joueur 1 si le joueur 2 joue de façon optimale, et deux choix mènent à une configuration verte, certainement gagnante pour le joueur 1. Le joueur 1 a donc la possibilité de jouer vers une configuration gagnante pour lui. Le nœud de départ est donc vert. Nous obtenons ce graphe :
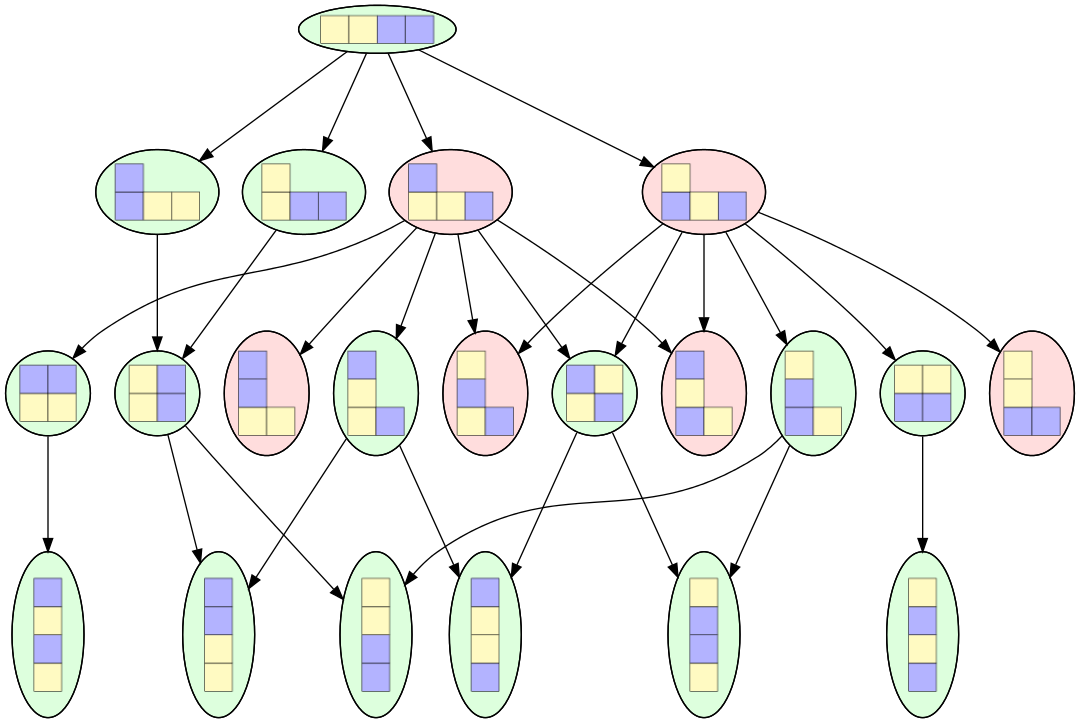
Figure 8
Cette dernière représentation nous indique que le joueur qui commence a la possibilité de gagner, s’il joue de façon optimale, en choisissant toujours de jouer vers un sommet vert, ce qu’il aura toujours la possibilité de faire. C’est donc la couleur du premier nœud (le nœud racine) qui indique lequel des deux joueurs a la possibilité de gagner si tout le monde joue de manière optimale.
L’algorithme que nous avons appliqué pour colorier le graphe a un nom. Il s’agit de l’algorithme du minimax. Pour le décrire en termes numériques, nous allons affecter un nombre plutôt qu’une couleur aux nœuds : le nœuds verts auront pour valeur 1 et les nœuds rouges pour valeur -1. S’il existait des configurations correspondant à un match nul, nous leur affecterions la valeur 0. L’algorithme du minimax fonctionnerait aussi avec ce cas supplémentaire.
Il est possible de déterminer la valeur (la couleur) de n’importe quel nœud en connaissant le numéro du tour (est-ce au joueur 1 de jouer ou au joueur 2), et la valeur de tous les descendants (qu’on appelle les nœuds fils) de ce nœud. En effet, si c’est au tour du joueur 1 de jouer, il suffit qu’un des fils ait pour valeur 1 pour que la valeur du nœud soit 1 (car le joueur peut jouer ce coup là). La valeur du nœud est donc le maximum des valeurs des fils : le seul cas où le nœud a pour valeur -1, c’est lorsque tous les fils ont pour valeur -1. Inversement si c’est au tour du joueur 2 de jouer, il suffit qu’un des fils ait pour valeur -1 pour que la valeur du nœud soit -1 (car le joueur 2 va joueur ce coup là). La valeur du nœud est donc le minimum des valeurs des fils : le seul cas où le nœud a pour valeur 1, c’est lorsque tous les fils ont pour valeur 1.
Reprenons. On affecte une valeur à chacun des autres nœuds ainsi :
- si le nœud correspond à un choix à faire pour le joueur 1, la valeur du nœud est le maximum des valeurs des fils
- si le nœud correspond à un choix à faire pour le joueur 2, la valeur du nœud est le minimum des valeurs des fils
Dans le cas où les nœuds n’ont pas de fils, c’est qu’un des deux joueurs est bloqué et on a directement la valeur du nœud, 1 ou -1.
Réduction de la taille du graphe
Pour optimiser un peu la représentation de nos graphes, nous allons remarquer que, pour une pile particulière, seule compte sa hauteur et la couleur de la brique supérieure. Ces deux configurations :
 et
et  sont équivalentes.
Les possibilités offertes pour les coups suivants sont en effet les mêmes (en l’occurrence, il n’y en a pas). Nous allons donc les identifier et systématiquement représenter les configurations en ne donnant que la hauteur des piles et la couleur supérieure. Les briques internes seront représentées en gris.
sont équivalentes.
Les possibilités offertes pour les coups suivants sont en effet les mêmes (en l’occurrence, il n’y en a pas). Nous allons donc les identifier et systématiquement représenter les configurations en ne donnant que la hauteur des piles et la couleur supérieure. Les briques internes seront représentées en gris.
Nous obtenons ainsi un nouveau graphe, un peu plus concis :
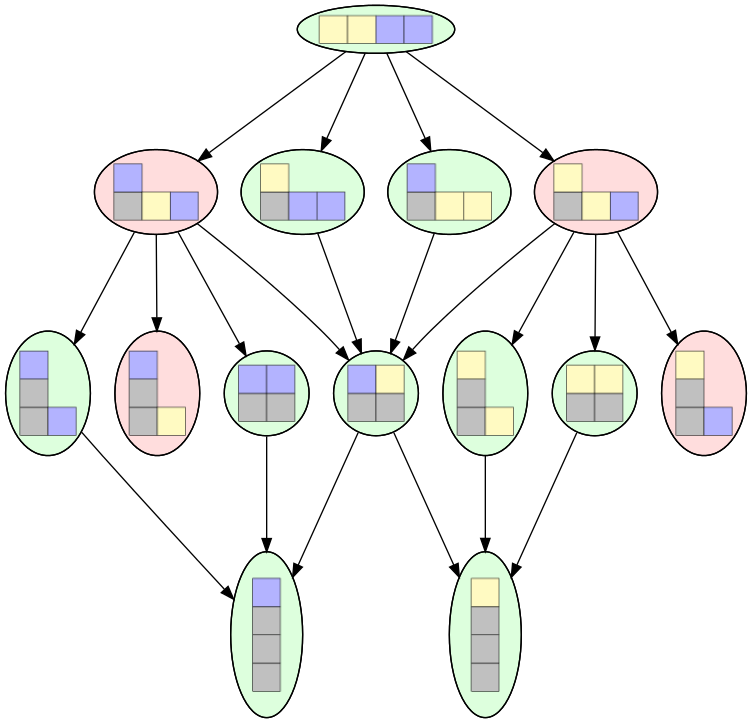
Figure 9
Bon… on ajoute des briques ?
Supposons maintenant qu’on dispose de 2 briques jaunes, 2 briques bleues, et 2 briques rouges. Gardons les mêmes règles. Que devient notre graphe ? Premièrement, il devient relativement grand (cliquez sur l’image pour l’agrandir) : pour 2×2 briques, le graphe comportait 14 nœuds et pour 3×2 briques, il en comporte maintenant 92.
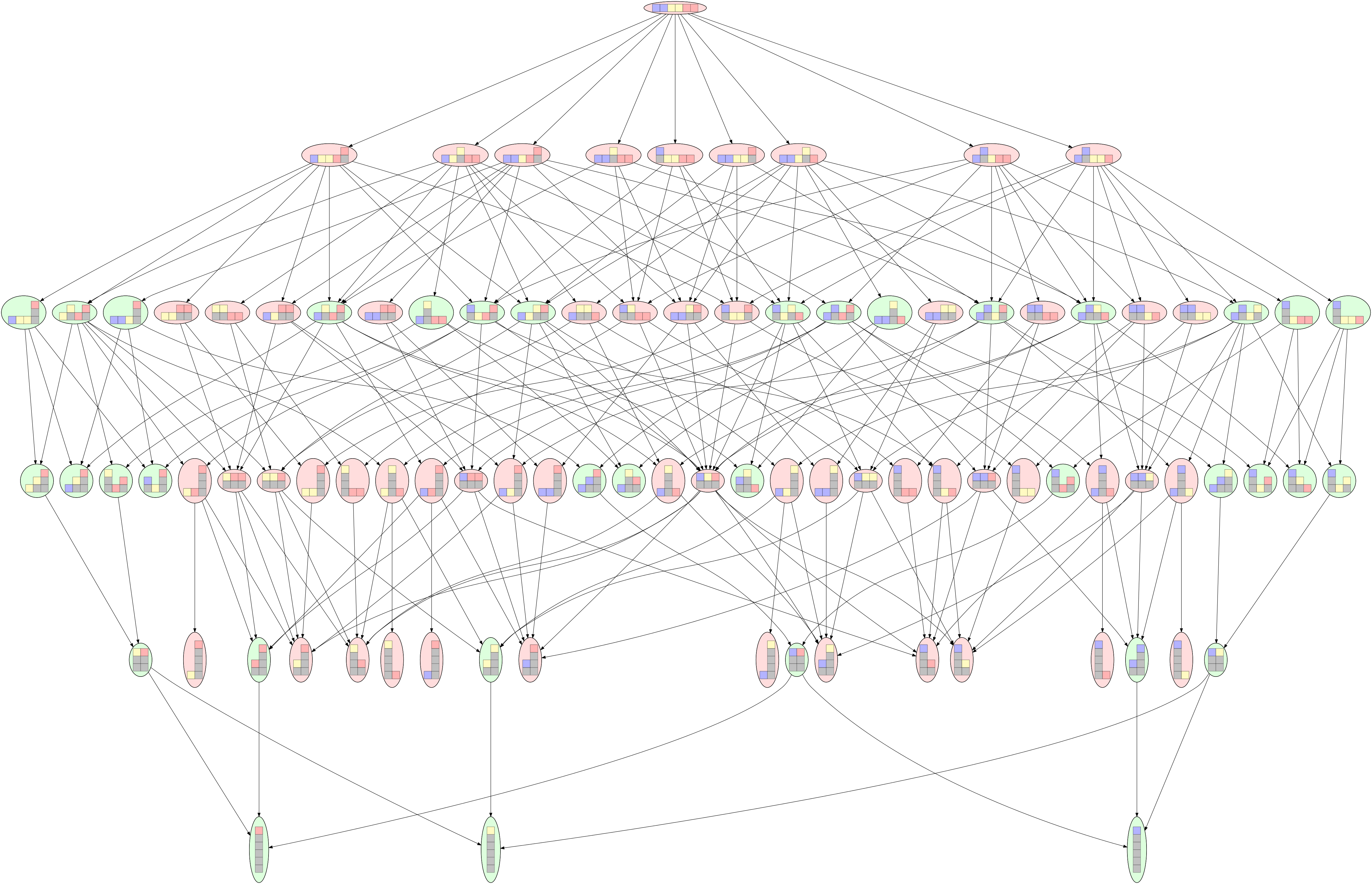
Figure 10
Et… mauvaise nouvelle pour le joueur 1 (celui qui commence), c’est le joueur 2 qui a cette fois une stratégie gagnante, puisque le nœud racine est rouge. Cela signifie que, quel que soit le premier coup joué par le joueur 1, de toutes manières, le joueur 2 aura la possibilité de gagner s’il joue bien.
Dans un souci de représenter un graphe un peu moins confus, puisque le joueur 2 a une stratégie gagnante, on peut ne conserver que les nœuds rouges du graphe. Le joueur 2 peut se servir de ce nouveau graphe pour décider quel coup jouer. Il suffit qu’il se débrouille (et ce sera toujours possible) pour se placer sur un des nœuds représentés dans ce nouveau graphe. Apprenez ce graphe par cœur et vous gagnerez toutes la parties de 3×2 briques si vous ne commencez pas à jouer…
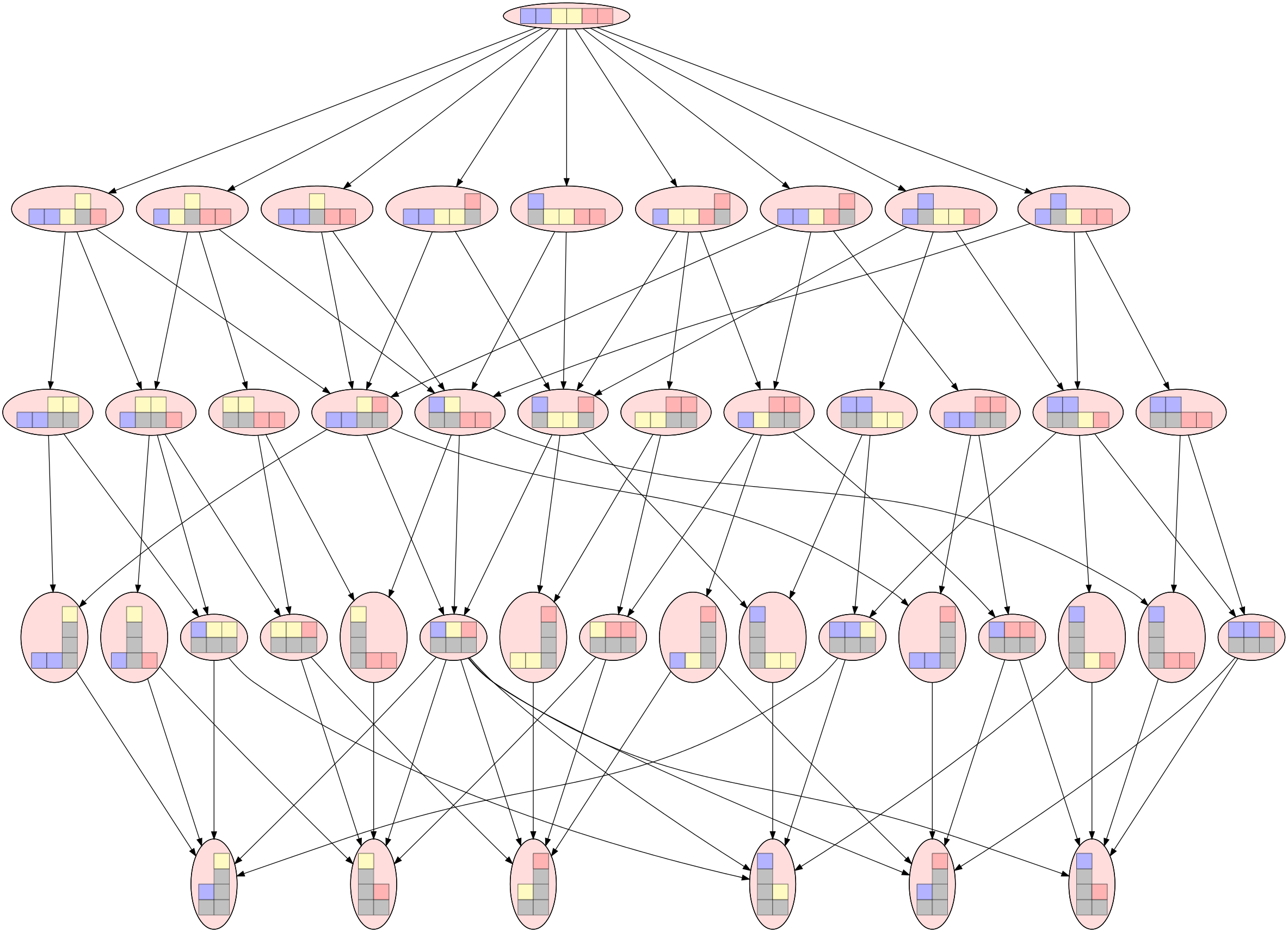
Figure 11
Qui va gagner la partie ?
Voici quelques résultats indiquant lequel, du joueur 1 (celui qui commence) ou du joueur 2, a une stratégie gagnante. Sur une ligne, on indique le nombre de couleurs, et sur une colonne, le nombre de briques par couleur. Dans toutes les parties, il y autant de briques de chaque couleurs (le nombre de briques total est donc le produit du numéro de ligne par le numéro de colonne), et au départ, aucune brique n’est empilé (toutes les piles sont de taille 1) :
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 2 | 1 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 1 | 1 | 2 | 1 |
| 4 | 1 | 1 | 2 | 1 | ||
| 5 | 1 | 2 | 2 | |||
| 6 | 2 | 2 |
On lit par exemple dans ce tableau qu’un gardant toujours deux briques par couleur, mais en ajoutant une couleur de plus (on a maintenant 4×2 briques), c’est à nouveau le joueur 1 qui a une stratégie gagnante (ligne 4, colonne 2, on lit : 1).
Qui veut coder ?
Pour ceux qui seraient désireux de coder les algorithmes dont il est question ici, voici quelques pistes, à utiliser avec Python ou à adapter à un autre langage. Ce sont celles que j’ai utilisées… pas forcément les meilleures.
La première chose à décider est comment représenter une configuration de jeu particulière. Sachant que modifier l’ordre des piles ne change pas la configuration, et que seule la taille de la pile et la couleur au sommet importe, on représente une pile par une chaîne de caractères comportant la lettre de la couleur de sommet (par exemple ‘r' pour rouge), puis le nombre de briques de la pile. Ainsi : r4 est une pile de 4 briques avec le sommet rouge. b3 est une pile de 3 briques avec le sommet bleu. Une configuration de jeu est représentée par une séquence (un tuple par exemple) de piles. La séquence aura autant d’éléments qu’il y a de piles dans la configuration. Et pour tenir compte du fait que l’ordre des piles n’a pas d’importances, on imposera que les éléments de la séquence soient triés (par exemple de manière alphanumérique, ce que fait la méthode sort()). Ainsi deux configurations équivalentes à l’ordre des piles près auront effectivement la même représentation.
Voici un exemple de configuration (‘b3’,‘r1’,‘r2’) comportant 3 piles. La première est composée de 3 briques, avec le sommet bleu, la seconde d’une seule brique rouge, et la troisième de 2 briques avec le sommet rouge.
On peut empiler la pile a (a est un indice) sur la pile b du tuple t, si t[a] et t[b] contiennent la même lettre ou le même nombre c’est à dire si t[a][0] == t[b][0] or t[a][1:] == t[b][1:]. Tester si un coup est possible est donc assez facile.
Voici à présent une fonction qui effectue un coup en jouant la pile i sur la pile j. Pour cela, on conserve la lettre de la pile j et on ajoute les chiffres des deux piles. On supprime la pile j, puis on retrie les piles :
def joue(pos, i, j):
pile = pos[i][0] + str(int(pos[j][1:]) + int(pos[i][1:]))
pos2 = list(pos)
pos2[i] = pile
del pos2[j]
return tuple(sorted(pos2))
La fonction qui précède est améliorable. Tout retrier est un peu excessif car il y a au pire une seule pile mal placée…
Voici maintenant une fonction qui donne l’ensemble des configurations qu’on peut atteindre à partir d’une configuration donnée. Stocker les configurations atteignables dans une ensemble est très pratique. Si deux coups distincts donnent la même configuration, celle-ci n’apparaîtra qu’une seule fois dans l’ensemble :
import itertools
def positions_suivantes(pos) :
""" ensemble des configuraitons atteignables depuis la position pos """
liste_coups = set()
n = len(pos)
# on envisage chaque coup i,j (poser i sur j)
for i,j in itertools.product(range(n),range(n)) :
if i == j : continue # on ne pose pas i sur i
# Si les couleurs de sommet ou la taille des piles sont égale s
if pos[i][1:] == pos[j][1:] or pos[i][0] == pos[j][0] :
# config obtenue si on pose i sur j
coup = joue(pos,i,j)
# et ajout de la config si elle n'est pas dans l'ensemble
liste_coups.add(coup)
return list(liste_coups)
Puis, voici l'algorithme du minimax proprement dit. Les numéros des joueurs sont ici 1 et -1, pour correspondre aux valeurs de nœuds.
def minimax(depart, dejacalcules, joueur):
# Si cette configuration est déjà connue, on ne
# la redéveloppe pas
if depart in dejacalcules:
return [dejacalcules[depart], depart, []]
# Ensemble des positions atteignables
filsa = positions_suivantes(depart)
# S'il n'y a pas de coup possible :
if len(filsa) == 0:
# si c'est au tour du joueur 1, le -1 a gagné, et
# inversement...
res = -joueur
dejacalcules[depart] = res
return [res, depart, []]
fils = []
val = []
valeur_noeud = 0
# Pour chaque configuration atteignable
for f in filsa:
# On lui applique l'algo du minimax
sousarbre = minimax(f, dejacalcules, -joueur)
val.append(sousarbre[0])
fils.append(sousarbre)
# val contient la liste des 1 et -1 associés à chaque connfiguration
# atteignable... Et voilà le principe du minimax :
if joueur == 1:
valeur_noeud = max(val)
else:
valeur_noeud = min(val)
dejacalcules[depart] = valeur_noeud
return [valeur_noeud, depart, fils]
Voici comment l’utiliser :
depart = ('b1', 'b1', 'r1', 'r1')
config = dict()
result = minimax(depart,config,1)
On obtient dans le dictionnaire config toutes les configurations atteignables dans la partie, avec le numéro du joueur qui gagne si le jeu est dans cette configuration :
pprint.pprint(config)
{('b1', 'b1', 'r1', 'r1'): 1,
('b1', 'b1', 'r2'): 1,
('b1', 'b2', 'r1'): -1,
('b1', 'r1', 'r2'): -1,
('b1', 'r3'): -1,
('b2', 'b2'): 1,
('b2', 'r1', 'r1'): 1,
('b2', 'r2'): 1,
('b3', 'r1'): -1,
('b4',): 1,
('r2', 'r2'): 1,
('r4',): 1}
La liste renvoyée par minimax est une liste de listes imbriquées, qui représente l’arbre (ou plutôt ici, le graphe) du jeu :
pprint.pprint(result)
[1,
('b1', 'b1', 'r1', 'r1'),
[[-1,
('b1', 'r1', 'r2'),
[[-1, ('b1', 'r3'), []],
[1, ('b2', 'r2'), [[1, ('r4',), []], [1, ('b4',), []]]],
[1, ('r2', 'r2'), [[1, ('r4',), []]]]]],
[-1,
('b1', 'b2', 'r1'),
[[-1, ('b3', 'r1'), []],
[1, ('b2', 'r2'), []],
[1, ('b2', 'b2'), [[1, ('b4',), []]]]]],
[1, ('b2', 'r1', 'r1'), [[1, ('b2', 'r2'), []]]],
[1, ('b1', 'b1', 'r2'), [[1, ('b2', 'r2'), []]]]]]</pre>
Quelques questions ouvertes (en tout cas pour moi…)
Voici quelques question qui sont apparues lors de la rédaction de ce billet, et pour lesquelles je n’ai pas de réponse. N’hésitez pas à proposer quelquechose en commentaires.
Peut-on facilement calculer le nombre de configurations possibles au bout de k coups ? Autrement dit, peut on calculer (par une formule) le nombre de nœud à chaque étage d’un arbre de jeu ? Par exemple, dans le cas d’un jeu avec 2 fois 2 briques, on des étages à 1, 4, 10 puis 6 configurations (figure 8) si on représente les couleurs des briques internes aux piles, ou bien 1, 4, 7 puis 2 configurations si on ne représente pas les couleurs des briques internes (figure 9).
Existe-t-il une formule qui, connaissant le nombre de couleurs et le nombres de briques de chaque, donne le numéro du gagnant ? Autrement dit, y a-t-il une formule qui permet de remplir le tableau donné un peu plus haut ?
À vos stylos… ou à vos ordis !
