Constante de Champernowne
Dans la catégorie des nombres curieux, la constante de Champernowne occupe une place particulière tant elle est simple à construire.
C’est un nombre irrationnel (un nombre irrationnel est un nombre qui ne peut pas être écrit comme le quotient de nombres entiers), compris entre 0 et 1, dont le développement en base 10 contient les nombres entiers écrits les uns à la suite des autre :
0.12345678910111213141516171819202122232425...
Nombre Univers
Entre autres propriétés, ce nombre possède, par construction, celle d’être un nombre univers (en base 10). Un nombre univers en base 10 est un nombre dont l’écriture en base 10 contient tous les entiers. Cette propriété est très curieuse, particulièrement à l’heure du numérique.
Songez par exemple au prochain titre phare de votre groupe favori. Ce titre de trois minutes sera enregistré sur un CD. La musique numérique, sur un CD, est enregistrée de manière non compressée. C’est simplement la suite des échantillons qui est gravée. Ces échantillons sont codés sur 16 chiffres binaires (une succession de 16 chiffres égaux à 0 ou 1).
La fréquence d’échantillonnage est 44,1kHz, ce qui signifie qu’il y a 44100 échantillons de 16 chiffres binaires par seconde et par oreille, si l’enregistrement est en stéréo. Trois minutes d’enregistrement correspondent donc à 16(chiffres)*2(oreilles)*44100(échantillons)*60(secondes)*3(minutes) = 254016000 chiffres binaires (environ un quart de milliards de chiffres).
Mis bout à bout, tous ces chiffres forment un nombre, compris entre 0 et $2^{254016000}-1 $. Ce dernier nombre est considérablement grand.
Quel que soit le nombre entier qui corresponde à notre single, il appartient à l’intervalle $[0..2^{254016000}-1]$ et figure à ce titre dans la constante de Champernowne. Celle-ci contient donc la musique d’un single que vous adorerez, mais qui n’est pas encore sorti. Mieux que ça, elle contient tous les singles de 3 minutes qui sont déjà sortis ou sortiront un jour, et on comprend aisément que la durée importe peu, et que la constante de Champernowne contient en fait toute la musique numérisée, toutes les photos numériques et tous les textes numériques qui ont existé ou existeront un jour (y compris ceux qui seront écrits par un écrivain qui n’est pas encore né).
Pour vous en convaincre, vous pourriez écrire un programme qui joue (sous forme de sons) la constante de Champernowne (il y aurait quelques détails techniques à régler, qui sont évoqués dans la dernière partie de ce billet). Il vous suffirait d’attendre pour entendre toute la musique connue ou à connaître. La difficulté résiderait dans le temps d’attente qui, vous l’aurez compris, serait bien trop long.
On peut alors se poser la question suivante (un peu tirée par les cheveux… je le reconnais) : n’y a t il pas moyen d’attendre un peu moins longtemps ?
Constante de Champernowne réduite
Dans la constante de Champernowne, par exemple, le nombre 2 figure très souvent, ainsi que 12 (au début, à cause de 1,2, puis plus loin quand on ajoute l’entier 12 au nombre). La cas de 12 est intéressant : au moment de l’écrire, après avoir écrit 11, nous savons que 12 a déjà été écrit (il suffit de se relire). Il est donc inutile de le rajouter pour qu’il soit présent. Le nombre obtenu en procédant ainsi est baptisé constante de Champernowne réduite : on ajoute chaque nombre s’il ne figure pas déjà dans l’écriture décimale. Dans l’exemple qui suit, un point (.) figure à chaque moment où un chiffre a été omis).
0.1234567891011..13141516171819202122..24252627282930..3233..35
Par construction ce nombre est aussi un nombre univers. Il contient aussi tous les entiers, soit parce qu’ils ont été ajoutés, soit parce qu’ils avaient déjà été écrits (en tant que concaténés d’autres nombres).
Quitte à écouter un nombre pour entendre toute la musique enregistrée ou qui sera enregistrée… il semble qu’il soit préférable d’écouter la constante réduite, puisqu’en première approximation elle a le même contenu, mais en moins de chiffres…
En y regardant plus attentivement, on verra que l’omission de l’entier 12 (puisqu’il figure déjà au début du nombre), nous prive de la suite 111213, qui est remplacée par 1113. Le nombre 21 apparaît donc plus tard dans la constante de Champernowne réduite que dans la constante de Champernowne. Est-ce exceptionnel ? Nous allons pouvoir le visualiser avec un petit programme.
Programme construisant les constantes
Le programme Python suivant permet de générer la constante de Champernowne réduite. Le paramètre est l’étape de construction :
def rchampernowne(n):
stri = ''
for i in range(1, n + 1):
if stri.count(str(i)) == 0:
stri = stri + str(i)
return '0.' + stri + '...'
À l’aide de cette fonction, et d’une fonction similaire pour construire la constante de Champernowne, on peut mesurer le numéro d’ordre de la décimale où chaque entier apparaît.
Dans la constante de Champernowne réduite : 0.1234567891011131415161718192021222425… l’entier 1 apparaît en position 0 (première décimale), l’entier 3 en position 2, l’entier 10 en position 9, l’entier 12 en position 0 et l’entier 23 (ou 234) en position 1.
La courbe suivante représente en abscisse les entiers de 1 à 500, et en ordonnée l’indice d’apparition de l’entier dans la constante de Champernowne (rouge) ou dans la constante de Champernowne réduite (bleu). Dans le cas où ces deux indices diffèrent, le plus petit est indiqué avec un point plus gros. La plupart des gros points sont donc bleus, indiquant qu’un nombre donné apparaît généralement plus tôt dans le développement décimal de la constante de Champernowne réduite. Les points rouges donnent les exceptions. Les premières exceptions sont obtenues pour les nombres : 21 32 43 112 121 132 142 152 162 172 182 213 221 223 231 232 243 253 263 273 283.
Ce sont les entiers qui apparaissent plus tôt dans le développement décimal de la constante de Champernowne que celui de la constante de Champernowne réduite.
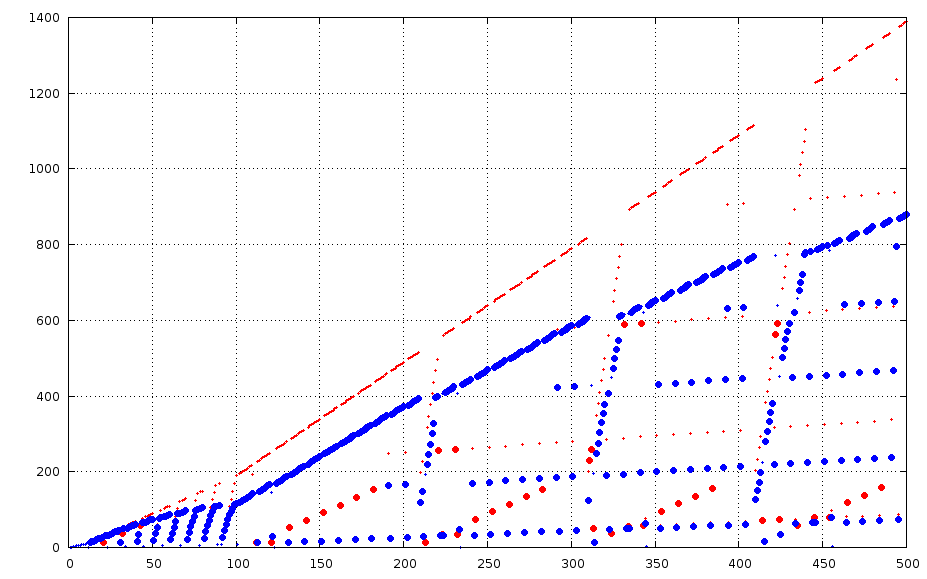
Indice d’apparition des entiers de 1 à 500
La courbe suivant donne les même indications mais pour tous les entiers jusqu’à 50000.
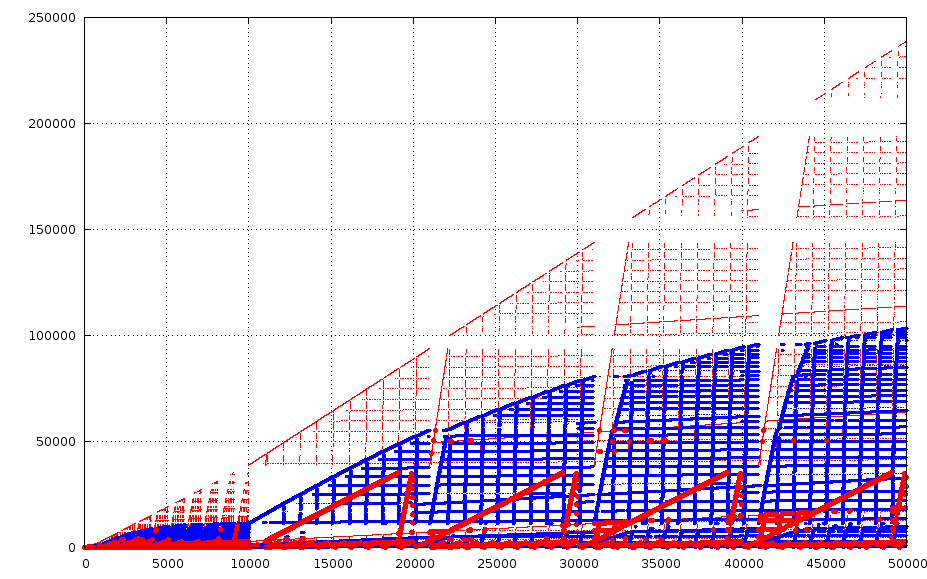
Indice d’apparition des entiers de 1 à 50000
Expérimentalement, il semblerait que dans 10% des cas environ, un nombre donné apparaisse plus tôt dans la constante de Champernowne que dans la constante de Champernowne réduite. Pas de chance si le morceau de musique recherché fait partie de ces 10%… :-)
Références
Vous pouvez retrouver la constante de Champernowne et la constante de Champernowne réduite sur l’extraordinaire encyclopédie en ligne des suites d’entiers OEIS : online encyclopedia of Integer Sequences
Le développement décimal des deux constantes constitue les suites : A033307 et A189823
Annexe : écouter la constante
Si on souhaitait vraiment écouter la constante de Champernowne pour y détecter un morceau de musique, il faudrait que son écriture, et l’ordre dans laquelle elle est lue soit adapté au codage numérique utilisé.
Pour simplifier, nous avons dans ce qui précède évoqué la constante en base 10, mais on peut bien sûr écrire des constantes équivalents dans une autre base. Pour correspondre à ce qu’on trouve sur un CD, il faudrait que chaque chiffre représente un échantillon et l’écriture adaptée serait la base 65536 ($2^{16}$), ce qui n’est pas très pratique.
Plus probablement, on se contenterait de dégrader le morceaux de musique, en considérant que chaque chiffre de la constante (entre 0 et 9 donc) est mis pour un échantillon musical (entre 0 et $2^{16}-1=65535$). Nous multiplierions donc chaque chiffre par 6550 (environ) avant d’envoyer le nombre obtenu vers le système audio. Nous obtiendrions alors une écoute mono très dégradée, mais néanmoins reconnaissable.
